GNN——图神经网络
Graph
首先,我们来了解一下什么是Graph。一般而言,图由三部分组成:
- V Vertex(or node) attributes,节点
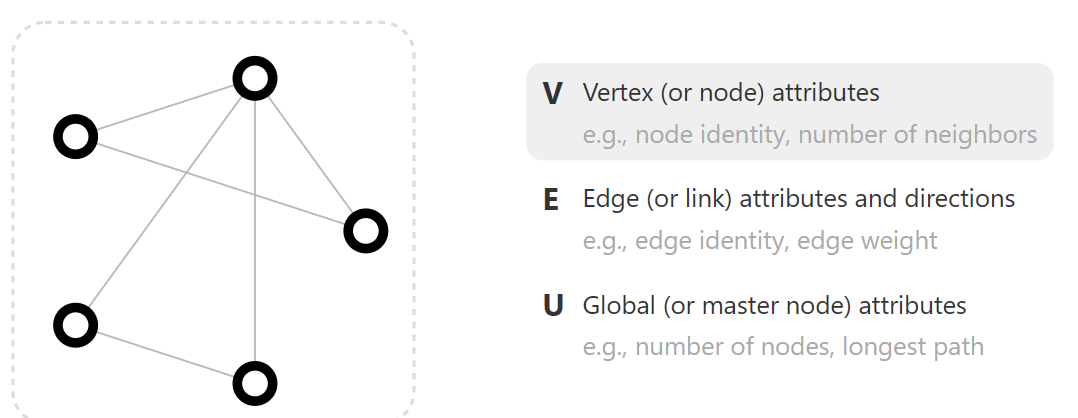
子属性包括节点标识,节点邻居数
- E Edge(or link) attributes and directions,边
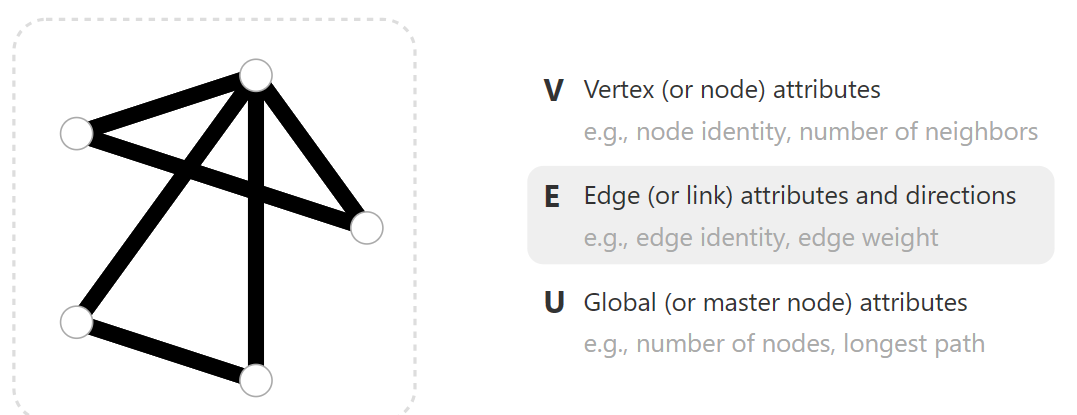
子属性包括边标识,边权重。
边可以包括有向边和无向边,有向边表示信息单方向流入,即从源节点流向目标节点;而无向边可以看为两个有向边的叠加,表示信息双向流动。

- U Global(or masternode) attributes,全局信息
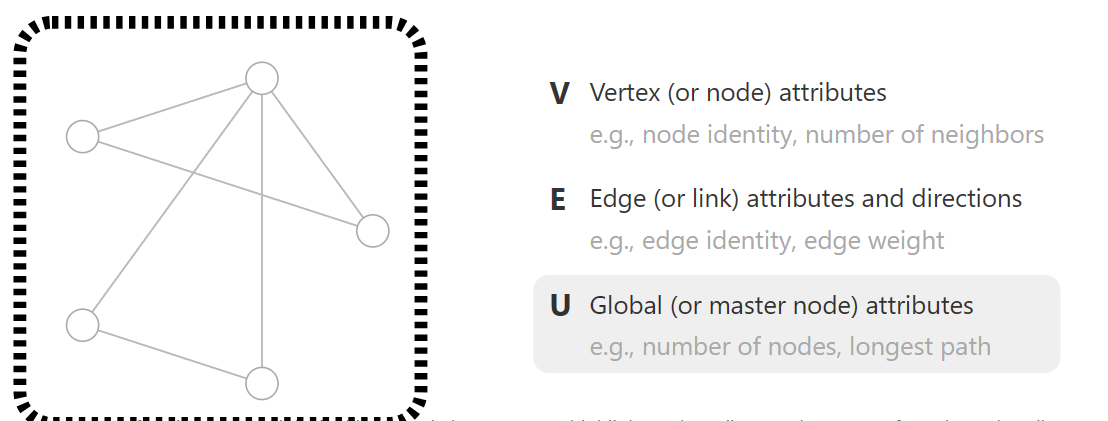
子属性包括节点数,最长路径
为了深入探究三者之间的关系,我们将每个节点信息、边信息和全局信息做Embedding,储存为向量形式。所以图神经网络的核心就是如何将我们想要的有效信息保存为向量以及如何建立神经网络从里面学习到有用的信息。
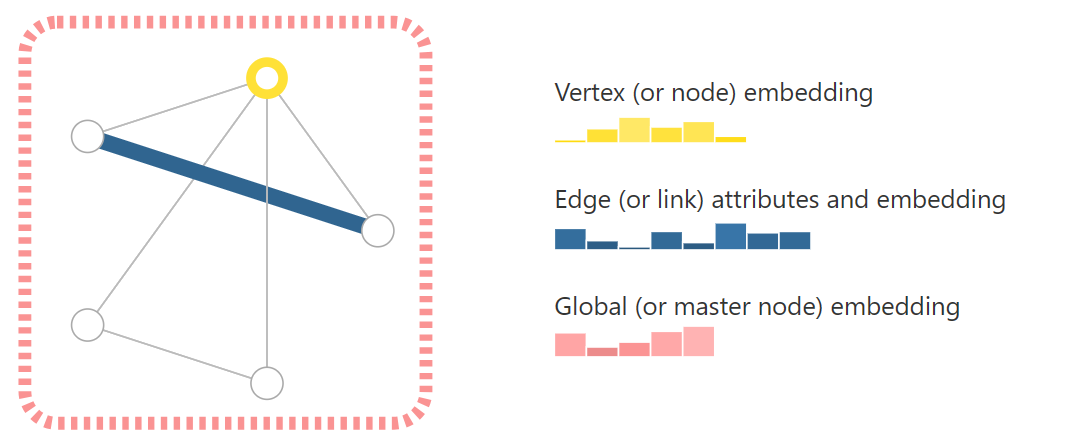
将数据转化为Graph
Images as graphs
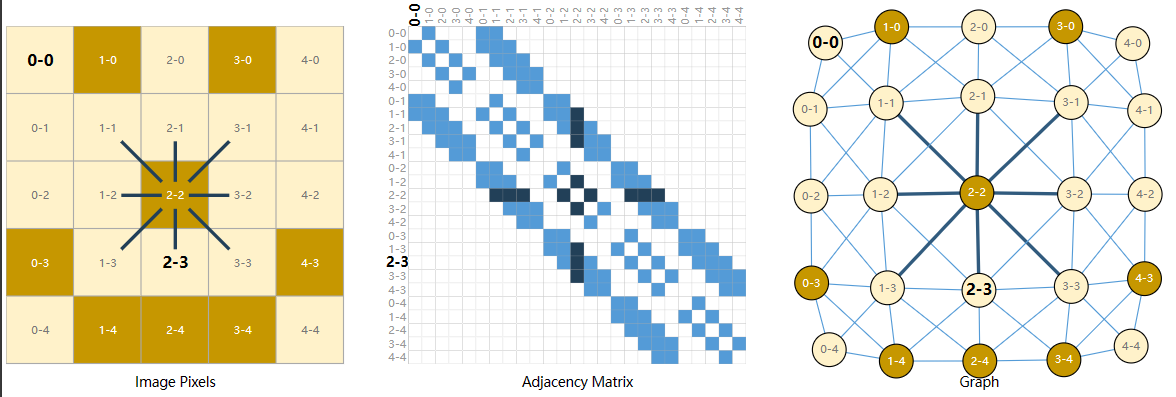
我们通常将图像视为具有图像通道的矩形网格,将它们表示为数组(例如,244x244x3)。
在这里,我们将图像理解为一种具有规则结构的Graph:每一个像素为一个节点,储存着代表RGB值的三维向量,并通过边连接到其他的像素,所以每一个非边界像素正好有8个邻居。
Text as graphs
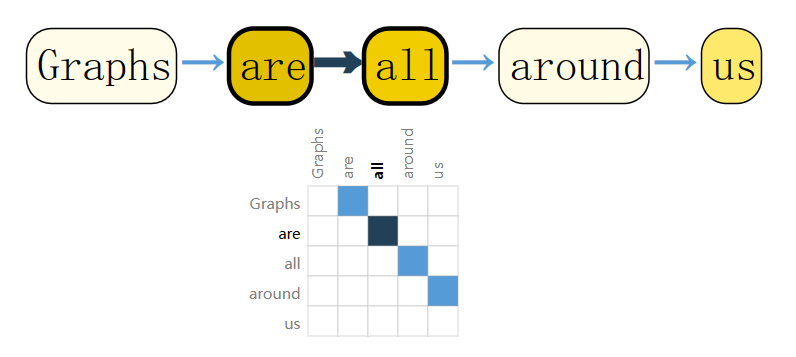
我们可以通过将索引与每个字符、单词或标记相关联,并将文本表示为这些索引的序列来数字化文本,这将创建一个简单的有向图,其中每一个字符或索引都是一个系欸但,并通过边连接到其后面的节点。
Others
除了上面提到的将图运用于CV和NLP领域的用法,我们还可以将图运用于其它各种数据内容中。
例如,我们可以将分子结构转换为图,其中每一个原子代表一个节点,每一个化学键代表一条边;
我们还可以将社交网络转换为图,每个人是一个节点,人与人之间的关系作为边;我们可以将论文的引文网络转换为图,将每篇论文看作一个节点,而一篇论文与另一篇论文之间的引用关系看作是一条有向边。
利用图进行预测
Graph的预测任务一般分为三种:graph-level, node-level, and edge-level.
Graph-level
在图级任务中,我们的目标是预测整个图的属性。例如,对于用图表表示的分子,我们可能想要预测该分子闻起来像什么,或者它是否会与与疾病有关的受体结合。
我们输入不含标签的Graph,经过学习后,神经网络会输出一个带有特定标签的图。
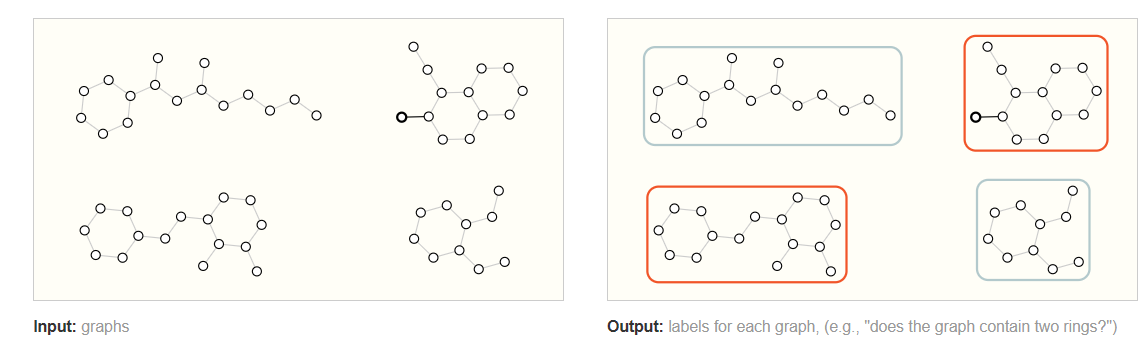
这类似于CIFAR的图片分类或者文本的标签分类问题。
Node-level task
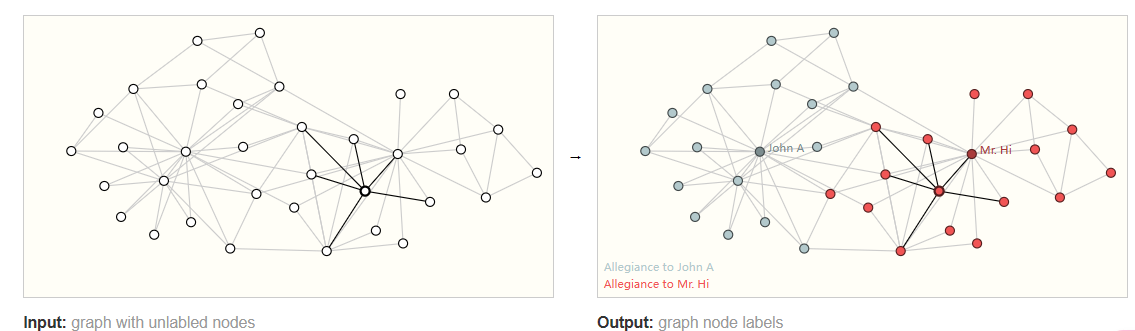
同理,对节点的预测一般是预测节点自身的一些属性和特征。
按照图像类比,节点级预测问题类似于图像分割,我们试图标记图像中每个像素的作用。对于文本,类似的任务是预测句子中每个单词的词性(例如名词、动词、副词等)。
Edge-level task
对边的预测一般是预测边连接哪些节点以及信息的传递方式。
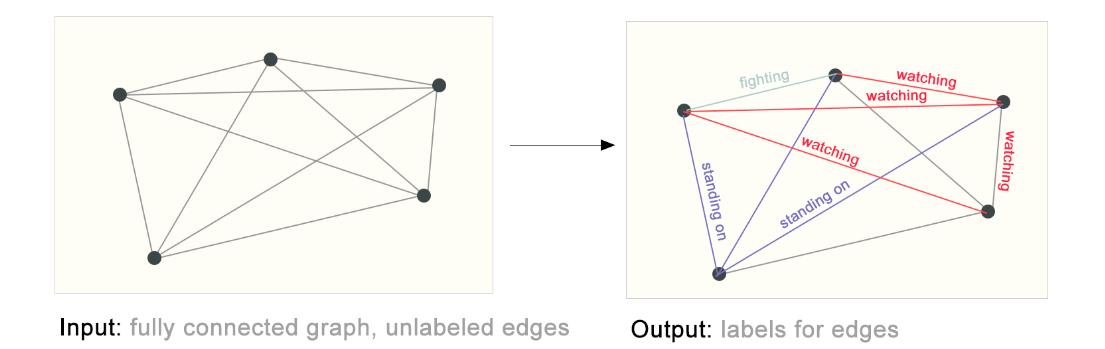
构建图神经网络
图的数据结构
在深度学习中,我们的数据一般以张量形式出现。对于图,最多包含四种类型的信息:节点、边、全局、连接性。
前三个相对而言比较简单,例如对于每个节点,我们都可以为其分配一个索引 $i$ ,这样我们可以构建出一个特征矩阵 $N$ , $node_{n}$ 的特征就储存在矩阵 $N$ 中。
困难的是如何表示图的连通性。一个直观的方式是使用邻接矩阵。
邻接矩阵(Adjacency Matrix)是用来表示图的一种常见方法之一。它是一个二维矩阵,其中的行和列分别代表图中的节点,而矩阵的元素表示节点之间是否存在边。
对于一个有向图,邻接矩阵的元素 $A_{ij}$ 表示从节点 $i$ 到节点 $j$ 是否存在一条边。如果存在边,则 $A_{ij}$ 的值通常为 1 或者表示边的权重;如果不存在边,则 $A_{ij}$ 的值通常为 0 或者其他表示不存在的值。在无向图中,如果节点 $i$ 与节点 $j$ 之间有边相连,则 $A_{ij}$ 和 $A_{ji}$ 都被设为 1(或者边的权重),否则为 0。
举例来说,对于一个无向图,如果存在节点 1 和节点 2 之间的边,则对应的邻接矩阵中的元素 $A_{12}$ 和 $A_{21}$ 都会被设为 1。而如果节点 1 和节点 3 之间没有边,则对应的 $A_{13}$ 和 $A_{31}$ 元素都会被设为 0。
邻接矩阵的优点是易于理解和实现,同时可以很方便地进行一些矩阵运算,比如矩阵乘法,从而在一些图算法中提供了便利。然而,对于大规模稀疏图来说,邻接矩阵会占用较多的内存空间,因为它会存储大量的零元素,因此在这种情况下,邻接表等其他数据结构可能更为高效。
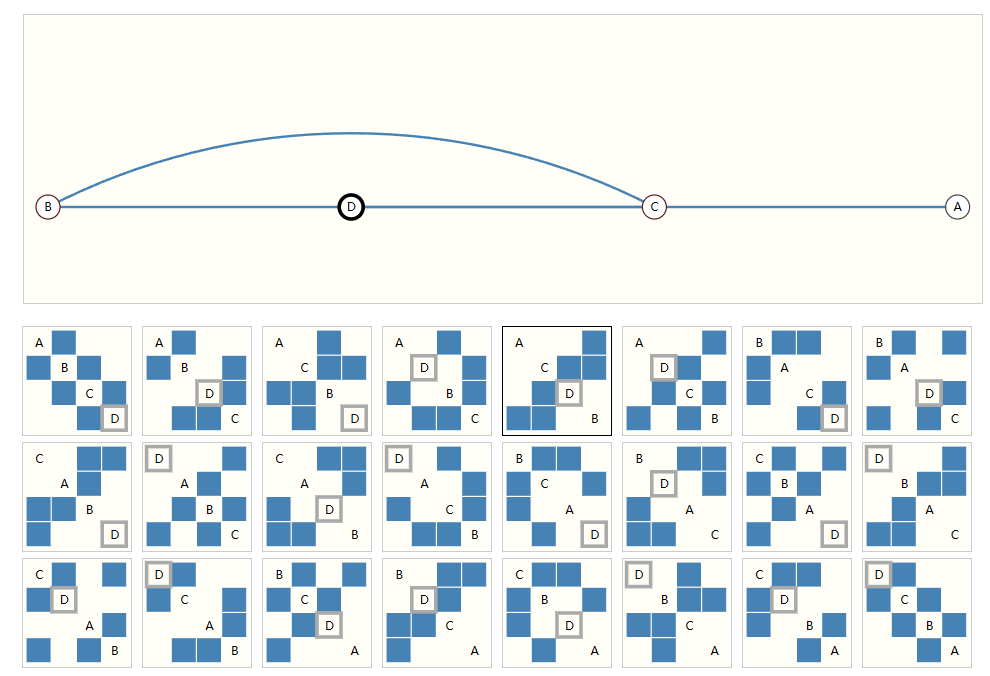
可以看见,表示四个节点之间的连接关系,我们就需要相当数量的矩阵来表示。
另一种方式是使用邻接表。
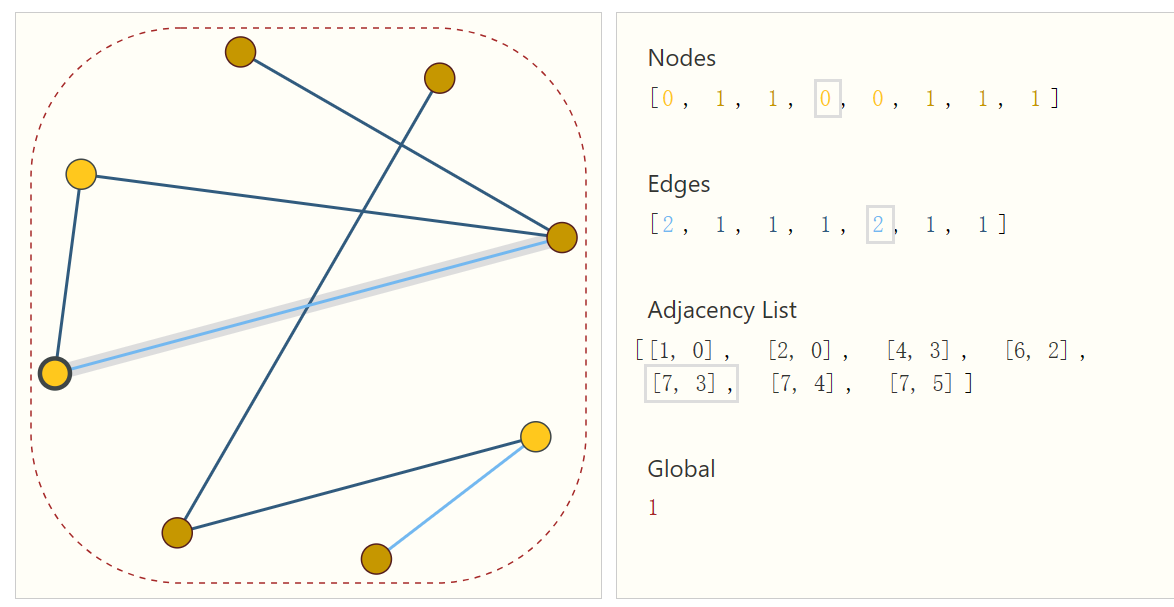
在表中,我们将每个node进行编码,然后使用一个tuple来储存两个node之间的连接关系。
上图中的节点、边和全局信息都可以用向量表示,而不一定只是标量。
图神经网络
图的描述是排列不变的矩阵格式,我们将描述使用图神经网络(GNN)来解决图预测任务。 GNN 是对图的所有属性(节点、边、全局上下文)的可优化变换,可保留图对称性(排列不变性)。
GNN 采用“图输入、图输出”架构,这意味着这些模型类型接受图作为输入,将信息加载到其节点、边和全局上下文中,并逐步转换这些嵌入,而不改变输入的连接性图形。
The simplest GNN
我们利用简单的MLP来构建GNN Layer
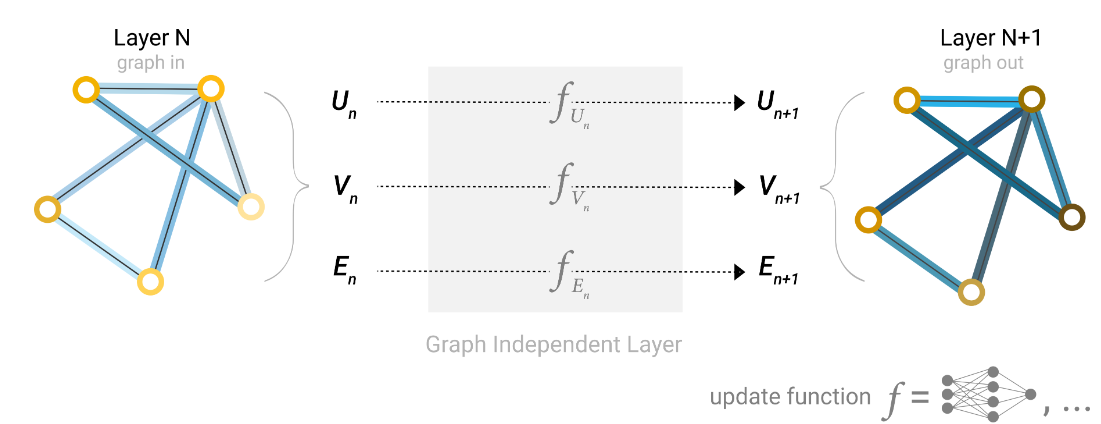
在经过多个全连接层的梯度下降和反向传播更新参数后,我们得到了一张不改变连接性但是改变节点和边、全局内容的图作为输出,我们可以使用与输入图相同的邻接表和相同数量的特征向量来描述 GNN 的输出图。
与神经网络模块或层一样,我们可以将这些 GNN 层堆叠在一起,获得更好的拟合效果。
多层感知机是一种常见的人工神经网络模型,由多个全连接层(Fully Connected Layer)组成,每个全连接层都包含多个神经元(或称为节点),相邻层之间的神经元之间全部连接。
在图神经网络中,MLP 通常被用作节点级别的特征转换器。具体来说,MLP 接收节点的特征作为输入,并通过多个全连接层来学习节点的新表示。这些新表示可以捕捉节点在图中的局部结构和全局信息,从而用于各种任务,如节点分类、节点预测等。
在 GNN 中,MLP 通常被应用在每个节点的特征更新过程中,以帮助节点表示学习更丰富的信息。例如,在图卷积网络(GCN)中,MLP 可以被用来对节点的邻居特征进行聚合和变换,以生成新的节点表示。在此过程中,MLP 的参数通常是可学习的,它们会通过反向传播算法来进行训练,以最大化模型的性能。
Pooling
如果我们进行的只是简单的分类任务,我们只需要对每个节点的embedding(即对应的张量)应用一个线性分类器即可。
但是这仅仅只利用了节点所储存的信息,并没有利用到边储存的信息和连接性。通过池化,我们可以收集边所储存的信息提供给节点进行预测。
池化的过程分两步进行:
- 对于要池化的每个项目,收集对应的张量并将它们连接成一个矩阵。
- 通过求和运算来得到收集的信息张量。

通过这种简单的叠加方式,我们可以将信息从节点传递到边或者从边传递到节点。
如果我们只有节点级特征,并且需要预测全局属性,则需要将所有可用的节点信息收集在一起并聚合它们。这类似于 CNN 中的全局平均池层。对于边缘也可以进行同样的操作。
我们用 $\rho$ 表示池化操作,并用 $pE_{n}\to V_{n}$ 表示从边收集信息到节点
Passing messages
消息传递分三个步骤进行:
- 对于每个节点,我们收集所有相邻节点的特征张量
- 通过聚合函数(如简单的相加)聚合收集到的信息
- 将聚合的信息通过更新函数传递
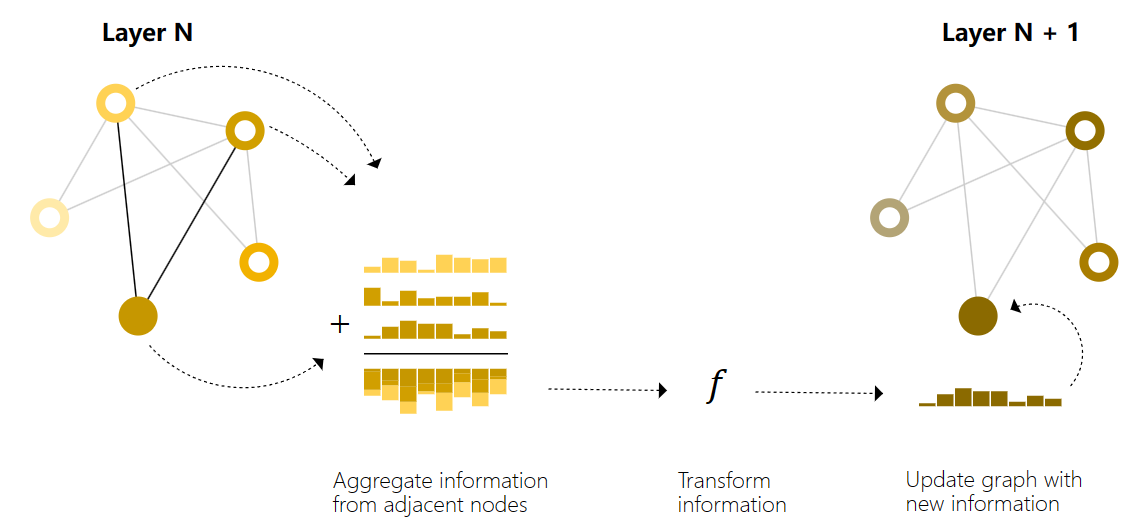
这让人想起标准卷积:本质上,消息传递和卷积是聚合和处理元素邻居信息以更新元素值的操作。在图形中,元素是节点,在图像中,元素是像素。然而,图中相邻节点的数量可以是可变的,这与每个像素具有固定数量的相邻元素的图像不同。
Learning edge representations
当我们想要对节点进行预测,但我们的数据集只有边缘信息时,我们在上面展示了如何使用池化将信息从边缘路由到节点,但仅限于模型的最终预测步骤。我们可以使用消息传递在 GNN 层内的节点和边之间共享信息。
我们可以采用与之前使用相邻节点信息相同的方式合并来自相邻边缘的信息,首先池化边缘信息,使用更新函数对其进行转换,然后存储它。
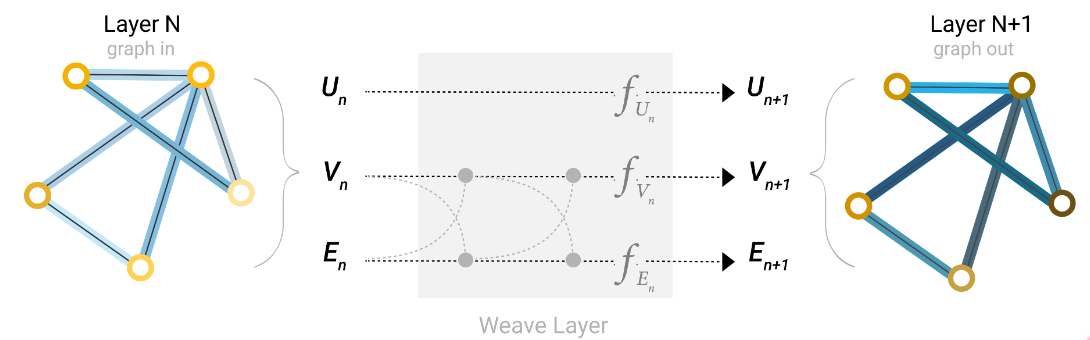
Adding global representations
到目前为止,我们描述的网络存在一个缺陷:即使我们多次应用消息传递,图中彼此相距较远的节点也可能永远无法有效地相互传输信息。
对于一个节点,如果我们有 k 层,信息将最多传播 k 步。
一种解决方案是让所有节点都能够相互传递信息。不幸的是,对于大型图,这很快就会变得计算成本高昂。此问题的一种解决方案是使用图 (U) 的全局表示,有时称为主节点或上下文向量,这个全局上下文向量连接到网络中的所有其他节点和边,并且可以充当它们之间传递信息的桥梁,构建整个图的表示。

在这个图中,所有图属性都已经学习了表示,因此我们可以在池化期间通过调节我们感兴趣的属性相对于其余属性的信息来利用它们。例如,对于一个节点,我们可以考虑来自相邻节点的信息、连接的边和全局信息。为了使新节点嵌入所有这些可能的信息源,我们可以简单地将它们连接起来。此外,我们还可以通过线性映射将它们映射到同一空间并添加它们或应用特征调制层,这可以被认为是一种特征化注意力机制。
其他类型的图
- 多边图:一对节点可以共享多种类型的边,当我们想要根据节点的类型对节点之间的交互进行不同的建模时,就会发生这种情况。
- 嵌套图:一个节点代表一个图,也称为超节点图。嵌套图对于表示层次结构信息很有用。