CNN——卷积神经网络

卷积神经网络(CNN)概述

整体架构分为：

  1. 输入层
  2. 卷积层
  3. 池化层
  4. 全连接层
  5. 激活函数

卷积神经网络由一个或多个卷积层、池化层以及全连接层等组成。与其他深度学习结构相比，卷积神经网络在图像等方面能够给出更好的结果。

img

卷积层

卷积运算

若一个 6*6的单通道图像与一个 3*3的卷积核进行卷积运算，那么从图像的左上角开始选取3*3的区域，将该区域的矩阵与卷积核的对应位置的元素相乘求和得到的结果便为输出矩阵的左上角元素。

$$\begin{bmatrix}
10& 10& 10& 0& 0& 0\\
10& 10& 10& 0& 0& 0\\
10& 10& 10& 0& 0& 0 \\
10& 10& 10& 0& 0& 0\\
10& 10& 10& 0& 0& 0 \\
10& 10& 10& 0& 0& 0
\end{bmatrix}*\begin{bmatrix}
1& 0 & -1\\
1& 0 & -1\\
1& 0 & -1
\end{bmatrix}=\begin{bmatrix}
0& 30& 30& 0\\
0& 30& 30& 0\\
0& 30& 30& 0\\
0& 30& 30& 0
\end{bmatrix}$$

卷积运算的目的是提取输入的不同特征，某些卷积层可能只能提取一些低级的特征，更多层的网络能从低级特征中迭代提取更复杂的特征。

卷积层的构成

参数：

  • size：卷积核的大小，选择一般有 1*1, 3*3, 5*5

    对于卷积核大小，一般采取奇数，这样做的目的是便于指出中心。

  • padding：一般为零填充，有Valid和Same两种方式。

    对于padding的解释：

    • 零填充：在图片像素的最外层加上若干层0值，若加1层，记为 p=1
      增加0是因为0在权重乘积运算中对最终结果不造成影响，也就避免了图片增加了额外的干扰信息。

    • Valid：不填充，保持原状，结果变小

    • Same：输出的大小与原图大小一致

  • stride：步长，通常默认为1

  • bias：偏置

对于每个卷积核，都会有一个偏置参数 $b$。

在卷积操作的计算中，偏置会与卷积核的加权和相加，并且会在整个输出图像上共享。具体地，输出图像中的每个像素值 $y$ 可以计算如下：

$$y = \sum_{i=1}^{M} \sum_{j=1}^{N} (w_{i,j} \cdot x_{i,j}) + b $$

其中 $w_{i,j}$ 是卷积核的权重，$x_{i,j}$ 是输入数据的对应像素值，$b$ 是偏置参数。

多通道卷积：

当输入有多个通道（channel）时（例如图片可以有RGB三通道），卷积核需要拥有相同的channel数，每个卷积核channel与输入层对应的channel进行卷积，将每个channel的卷积结果按位相加得到最终的 Feature Map。

多卷积核卷积：

当有多个卷积核时，可以学习到多种不同的特征，对应产生包含多个channel的 Feature Map，例如当拥有两个kernel时，输出结果会有两个channel。

得到的特征图大小不变，数量变多。

这里的多少个卷积核也可以理解为多少个神经元。

例子：

假设我们有一张 $200\times 200$ 的图片，10个kernel，size=3*3，channel=3(计算RGB图片)，并且只有一层卷积，步长为1，那么参数的计算过程为：

对于每个kernel，有 $3\times 3\times 3+1$ 个参数

所以总共有 $28\times 10=280$ 个参数。

零填充的层数 $P=\frac{(N-1)\times s+F-N}{2}=\frac{199+3-200}{2}=1$

$N$ 为图片大小， $s$ 为stride， $F$ 为卷积核大小

池化层

池化层主要对卷积层学习到的特征图进行亚采样（subsampling），主要有两种：

  1. 最大池化：Max Pooling，取窗口内的最大值作为输出
  2. 平均池化：Avg Pooling，取窗口内所有值的均值作为输出

意义在于：

  • 降低了后续网络层的输入维度，缩减模型大小，提高计算速度
  • 提高了Feature Map的鲁棒性，防止过拟合

一般来说池化操作即为选取图片的一个固定大小的区域（窗口），在该区域中得到一个代表这个区域的数值，并总和输出结果。

窗口设置：一般大小为 $2\times 2$, $stride=2$ 。

在处理多通道输入数据时，池化层对每个输入通道分别池化，而不是像卷积层那样将各个通道的输入相加。这意味着池化层的输出和输入的通道数是相等。

全连接层

全连接层的目的是将卷积和池化层提取的特征进行整合，并输出到最终的输出层，以进行分类、回归或其他任务。

卷积层＋激活层＋池化层可以看作是CNN的特征学习/特征提取层，而学习到的特征最终运用于模型任务，一般来说分为分类或回归。

  • 先对所有 Feature Map 进行扁平化（flatten，即reshape成 $1\times N$ 的向量）

  • 再接一个或多个全连接层，进行模型学习

img

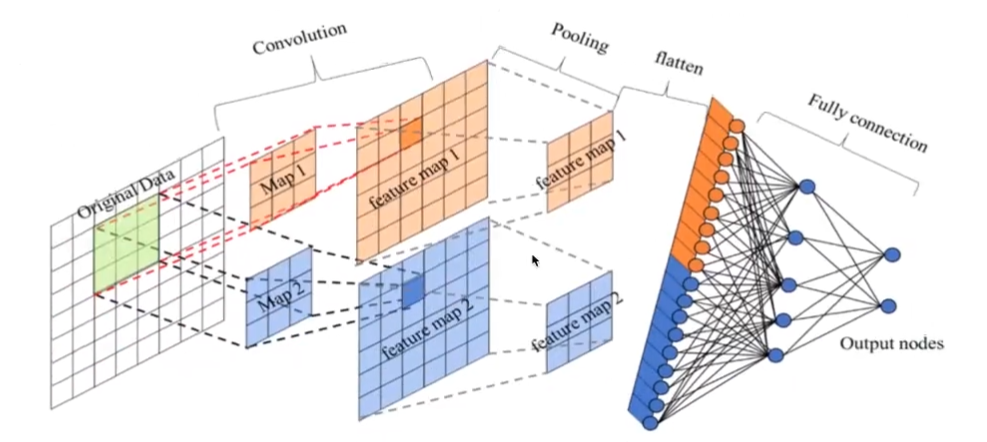
构建CNN实现图片分类

分类器任务和数据介绍

  • 构造一个将不同图像进行分类的神经网络分类器，对输入的图片进行判别并完成分类
  • 采用 CIFAR10 数据集作为原始图片数据

CIFAR10数据集介绍：数据集中每张图片的尺寸是 3*32*32 ，代表彩色三通道。
CIFAR10数据集总共有10种不同的分类，分别是 “airplane”,”automobile”,”bird”,”cat”,”deer”,”dog”,”frog”,”horse”,”ship”,”truck”

img

训练分类器的步骤

  1. 使用torchvision下载CIFAR10数据集
  2. 定义卷积神经网络
  3. 定义损失函数
  4. 在训练集上训练模型
  5. 在测试集上测试模型

构建神经网络的基本步骤

  • 使用PyTorch构建神经网络，主要的工具都在torch.nn包中
  • nn依赖于autograd来定义模型，并对其自动求导

主要步骤：

  1. 定义一个拥有可学习参数的神经网络
  2. 遍历训练数据集
  3. 处理输入数据使其流向神经网络
  4. 计算损失值
  5. 将网络参数的梯度进行反向传递
  6. 以一定的规则更新网络的权重

下载数据集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import torch
import torchvision
import torchvision.transforms as transforms

# 下载数据集并对图片进行调整，因为torchvision数据集的输出是PILImage格式，数据域在[0, 1]。
# 我们将其转换为标准数据域[-1, 1]的张量格式
transform = transforms.Compose(
    [transforms.ToTensor(),
     transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)

trainloader = torch.utils.data.DataLoader(trainset, batch_size=4, shuffle=True, num_workers=2)

testset = torchvision.datasets.CIFAR10(root='./data', train=False, download=True, transform=transform)

testloader = torch.utils.data.DataLoader(testset, batch_size=4, shuffle=False, num_workers=2)

classes = ('plane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck')

对这段代码的解释：

1
2
3
transform = transforms.Compose(
    [transforms.ToTensor(),
     transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])

创建一个数据转换管道，使用 transforms.Compose()。

它按顺序应用两个转换到输入图像：

  • transforms.ToTensor(): 将PIL图像或numpy.ndarray转换为PyTorch张量。图像数据被转换为张量并标准化到范围[0, 1]。
  • transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)): 使用均值和标准差对张量图像进行归一化。这将使用每个通道（R、G、B）的均值和标准差值（0.5、0.5、0.5）对图像张量进行归一化。归一化公式为 $\frac{(input - mean)}{std}$
1
trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)

使用torchvision中的CIFAR-10数据集创建一个训练数据集对象（trainset）。它指定了以下参数：

  • root=’./data’: 指定数据集将被存储的目录。
  • train=True: 表示这是训练集。
  • download=True: 如果数据集尚未下载，则下载数据集。
  • transform=transform: 对数据集应用前面定义的转换。
1
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4, shuffle=True, num_workers=2)

创建一个用于训练数据集的数据加载器（trainloader）。它指定了以下参数：

  • trainset: 要加载的数据集对象。
  • batch_size=4: 将批次大小设置为4，这意味着在训练期间每次加载4张图像。
  • shuffle=True: 在每个epoch之前对数据进行洗牌，以引入随机性并避免模型学习数据的顺序。
  • num_workers=2: 用于数据加载的子进程数。在这里，将使用2个子进程加载数据。
1
classes = ('plane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck')

此行定义了与CIFAR-10数据集中的10个类别相对应的类标签。稍后将使用这些标签进行预测和评估。

定义卷积神经网络

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import torch
import torch.nn as nn
import torch.nn.functional as F

# 定义卷积神经网络
class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.pool = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(16*5*5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        x = self.view(-1, 16*5*5)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

一些注释

对于 init 函数：

  • 第一个卷积层 self.conv1 输入通道数为3（因为输入图像有3个通道，通常为RGB），输出通道数为6，卷积核大小为5x5。
  • 第一个最大池化层 self.pool 使用2x2的池化窗口进行池化操作，步长为2。
  • 第二个卷积层 self.conv2 输入通道数为6（即第一个卷积层的输出通道数），输出通道数为16，卷积核大小为5x5。
  • 第一个全连接层 self.fc1 的输入大小为16x5x5，输出大小为120。
  • 第二个全连接层 self.fc2 的输入大小为120，输出大小为84。
  • 第三个全连接层 self.fc3 的输入大小为84，输出大小为10（因为通常在分类问题中，输出层的大小对应着类别的数量）。

对于 forward 函数：

  • 首先将输入张量 x 传递给第一个卷积层 self.conv1，然后应用 ReLU 激活函数，并通过最大池化层 self.pool 进行池化操作。
  • 接着将经过第一个池化层处理后的数据传递给第二个卷积层 self.conv2，然后再次应用 ReLU 激活函数，并再次通过最大池化层进行池化操作。
  • 将经过两个卷积层和池化层处理后的数据 x 展平为一维张量。
  • 将展平后的数据传递给第一个全连接层 self.fc1，并应用 ReLU 激活函数。
  • 将第一个全连接层的输出传递给第二个全连接层 self.fc2，再次应用 ReLU 激活函数。
  • 最后将第二个全连接层的输出传递给输出层

定义损失函数

1
2
3
# 定义损失函数
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)

采用交叉熵损失函数和梯度下降算法。

训练模型

  • 采用梯度下降的优化算法，都需要很多个轮次的迭代训练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 在训练集上训练模型
    for epoch in range(2):    # 遍历两遍数据集
        running_loss = 0.0
        for i, data in enumerate(trainloader, 0):
            # data中包含输入图像张量inputs，标签张量labels
            inputs, labels = data
            # 梯度归零
            optimizer.zero_grad()
            # 输入图像张量进网络，得到输出张量outputs
            outputs = net(inputs)
            # 利用网络的输出output和标签labels计算损失值
            loss = criterion(outputs, labels)
            # 反向传播+参数更新
            loss.backward()
            optimizer.step()
            # 打印轮次和损失值
            running_loss += loss.item()
            if (i + 1) % 2000 == 0:
                print('[%d, %5d] loss: %.3f' % (epoch + 1, i + 1, running_loss / 2000))
                running_loss = 0.0
    print('Finished Training')
    # 保存模型
    PATH = './cifar10_net.pth'
    torch.save(net.state_dict(), PATH)

训练结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
'''
[1,  2000] loss: 2.235
[1,  4000] loss: 1.860
[1,  6000] loss: 1.651
[1,  8000] loss: 1.573
[1, 10000] loss: 1.513
[1, 12000] loss: 1.477
[2,  2000] loss: 1.395
[2,  4000] loss: 1.369
[2,  6000] loss: 1.333
[2,  8000] loss: 1.325
[2, 10000] loss: 1.311
[2, 12000] loss: 1.295
Finished Training
'''

在测试集上测试模型

第一步，展示测试集中的若干图片

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 展示图片
dataiter = iter(testloader)
images, labels = dataiter.next()

def imshow(img):
    img = img / 2 + 0.5
    npimg = img.numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))
    plt.show()

# 打印原始图片
imshow(torchvision.utils.make_grid(images))
# 打印真实标签
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))

代码解读：

  • dataiter = iter(testloader): 创建了一个迭代器 dataiter，用于迭代测试数据加载器 testloader，以便逐批获取测试数据。

  • images, labels = next(dataiter): 使用 next() 函数从 dataiter 中获取下一批测试数据，其中 images 是一个包含了一批图像的张量，labels 是这批图像对应的真实标签。

  • def imshow(img): 定义了一个函数 imshow，用于展示图像。

  • img = img / 2 + 0.5: 对输入的图像数据进行处理，将其从标准化后的张量格式转换回原始图像的像素值范围，即从 [-1, 1] 转换为 [0, 1]。

  • npimg = img.numpy(): 将张量类型的图像数据转换为 NumPy 数组，因为 matplotlib 库接受的是 NumPy 数组格式的图像数据。

  • plt.imshow(np.transpose(npimg, (1, 2, 0))): 使用 imshow 函数展示图像。

(1, 2, 0): 这是一个元组，指定了数组的维度顺序。在这个元组中，每个数字表示了原始数组的一个维度在新数组中的位置。因此，(1, 2, 0) 意味着将原始数组的第 1 维移动到新数组的第 0 个位置，第 2 维移动到新数组的第 1 个位置，原始数组的第 0 维移动到新数组的第 2 个位置。

在图像处理中，一般图像数组的维度顺序是 (通道数, 高度, 宽度)，即 (channels, height, width)，其中 channels 表示图像的通道数，比如 RGB 图像中通常是 3。而 imshow 函数默认会将最后一个维度视为通道维度，所以需要用 np.transpose() 来调整数组的维度顺序以匹配 imshow 的预期输入格式，即 (height, width, channels)。

  • plt.show(): 显示图像。

  • imshow(torchvision.utils.make_grid(images)): 调用 imshow 函数，将一批图像组合成一个网格并展示出来。

  • print(‘GroundTruth: ‘, ‘ ‘.join(‘%5s’ % classes[labels[j]] for j in range(4))): 打印出这批图像对应的真实标签。使用了列表推导式，将每个图像的真实标签转换为对应的类别名称，并使用空格连接起来，最后打印出来。

输出结果：
img

1
GroundTruth:    cat  ship  ship plane

第二步，加载模型对测试图片进行预测

1
2
3
4
5
6
7
8
9
net = Net()
# 加载保存的状态字典
net.load_state_dict(torch.load(PATH))
# 进行预测
outputs = net(images)
# 采用计算出概率最大的为类别
_, predicted = torch.max(outputs, 1)
# 打印结果
print('Prediced: ', ' '.join('%5s' % classes[predicted[j]] for j in range(4)))

运行结果：

1
2
GroundTruth:    cat  ship  ship plane
Prediced:    cat automobile plane plane

稍有误差。。。加大epoch！

全部测试集结果：

1
2
3
4
5
6
7
8
9
10
11
12
# 跑一遍全部测试集
correct = 0
total = 0
with torch.no_grad():
    for data in testloader:
        images, labels = data
        outputs = net(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print('Accuracy: %d %%' % (100 * correct / total))
1
Accuracy: 54 %

准确率为54%，说明模型初步具备分类能力，还有较大提升空间。

我们可以计算模型在哪些类别上表现更好，在哪些类别上表现更差，也可以分类别进行准确率计算，此处不再演示。

把学习率由 1e-3 修改为 1e-4, 并网络参数量增加如下代码所示:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class ImageClassification(nn.Module):

    def __init__(self):
        super(ImageClassification, self).__init__()
        self.conv1 = nn.Conv2d(3, 32, stride=1, kernel_size=3)
        self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2)
        self.conv2 = nn.Conv2d(32, 128, stride=1, kernel_size=3)
        self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
        self.linear1 = nn.Linear(128 * 6 * 6, 2048)
        self.linear2 = nn.Linear(2048, 2048)
        self.out = nn.Linear(2048, 10)


    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = self.pool1(x)
        x = F.relu(self.conv2(x))
        x = self.pool2(x)
        # 由于最后一个批次可能不够 32，所以需要根据批次数量来 flatten
        x = x.reshape(x.size(0), -1)
        x = F.relu(self.linear1(x))
        x = F.dropout(x, p=0.5)
        x = F.relu(self.linear2(x))
        x = F.dropout(x, p=0.5)
        return self.out(x)

经过训练，模型在测试集的准确率由 0.57，提升到了 0.93。

Deep Learning
CNN——卷积神经网络
https://fabulous1496.github.io/2024/03/18/CNN/
作者
Fabulous
发布于
2024年3月18日
许可协议