RNN——循环神经网络

RNN概述

当我们在理解一句话意思时，孤立的理解这句话的每个词是不够的，我们需要处理这些词连接起来的整个序列；当我们处理视频的时候，我们也不能只单独的去分析每一帧，而要分析这些帧连接起来的整个序列。

首先看一个简单的循环神经网络如，它由输入层、一个隐藏层和一个输出层组成：

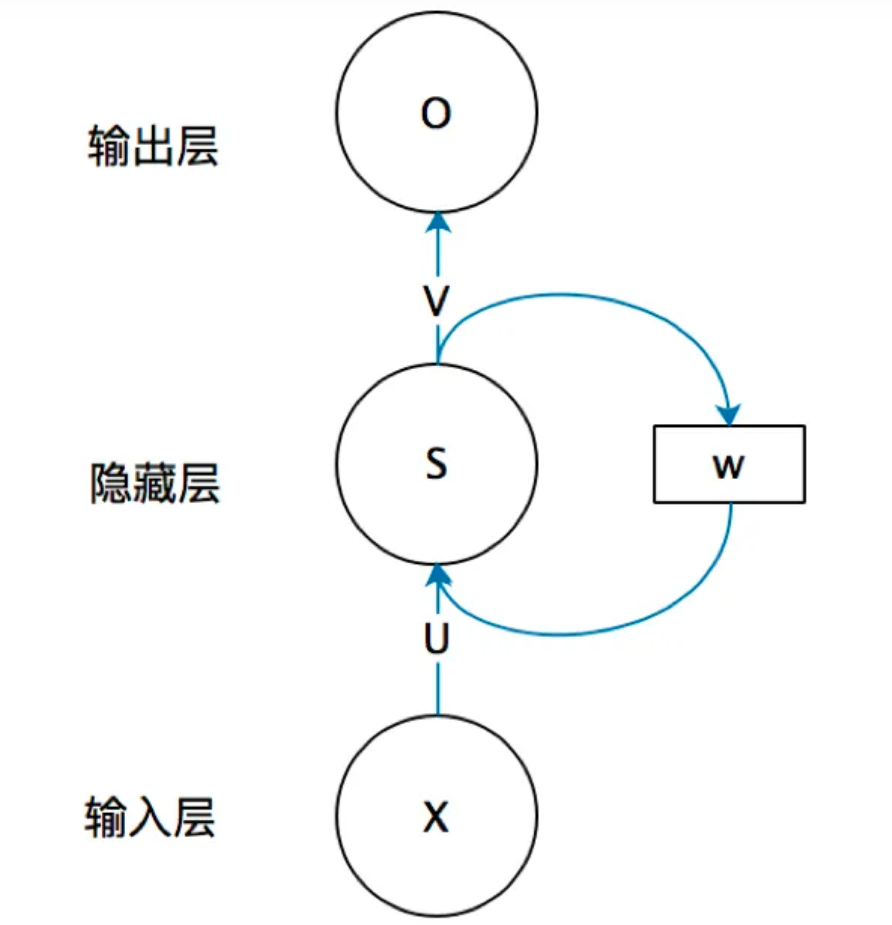
其中，$O$ 是一个向量，代表输出层的值；$V$ 是隐藏层到输出层的权重矩阵，$U$ 是输入层到隐藏层的权重矩阵。

循环神经网络的隐藏层的值S不仅仅取决于当前这次的输入 $X$ ，还取决于上一次隐藏层的值 $S’$ 。权重矩阵 $W$ 就是隐藏层上一次的值作为这一次的输入的权重。

按时间线展开，我们可以得到下图：

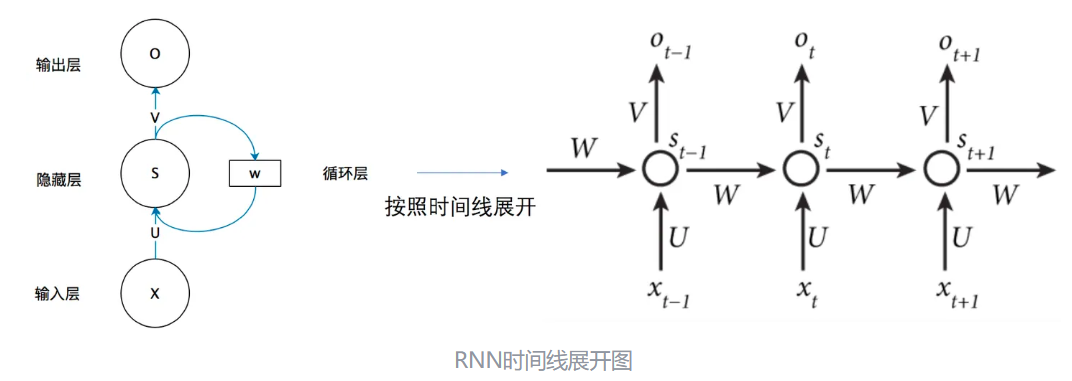
不考虑bias的情况下，公式可以简化为：

$$\begin{cases}
O_{t} = g(V \ldotp S_{t}) \\
S_{t} = f(U \ldotp X_{t}+W \ldotp S_{t-1})
\end{cases}$$

举个例子：
第一步: 用户输入了”What time is it ?”, 我们首先需要对它进行基本的分词, 因为RNN是按照顺序工作的, 每次只接收一个单词进行处理.

第二步: 首先将单词”What”输送给RNN, 它将产生一个输出 $O_{1}$.

第三步: 继续将单词”time”输送给RNN, 但此时RNN不仅仅利用”time”来产生输出 $O_{2}$ , 还会使用来自上一层隐层输出 $O_{1}$ 作为输入信息.

第四步: 重复这样的步骤, 直到处理完所有的单词.

第五步: 最后，将最终的隐层输出 $O_{5}$ 进行处理来解析用户意图.

RNN模型的分类

按照输入和输出的结构进行分类:

N vs N - RNN：输入和输出序列是等长的。
N vs 1 - RNN：输出是一个单独的值而不是序列。
1 vs N - RNN：输入不是序列而输出为序列
N vs M - RNN：不限输入输出长度的RNN结构，由编码器和解码器两部分组成, 两者的内部结构都是某类RNN, 它也被称为seq2seq架构。输入数据首先通过编码器, 最终输出一个隐含变量c, 之后最常用的做法是使用这个隐含变量c作用在解码器进行解码的每一步上, 以保证输入信息被有效利用。

按照RNN的内部构造进行分类:

传统RNN
LSTM
Bi-LSTM
GRU
Bi-GRU

传统RNN

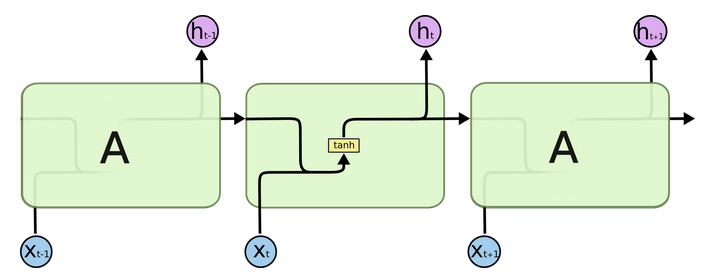
接下来使用h(t)来代表隐藏层的输出

我们把目光集中在中间的方块部分, 它的输入有两部分, 分别是 $h(t-1)$ 以及 $x(t)$, 代表上一时间步的隐层输出, 以及此时间步的输入, 它们进入RNN结构体后, 会”融合”到一起, 这种融合我们根据结构解释可知, 是将二者进行拼接, 形成新的张量 $[x(t), h(t-1)]$ , 之后这个新的张量将通过一个全连接层(线性层), 该层使用 $tanh$ 作为激活函数, 最终得到该时间步的输出 $h(t)$, 它将作为下一个时间步的输入和 $x(t+1)$ 一起进入结构体，以此类推。

$$h_{t} = tanh(W_{t}[X_{t},h_{t-1}]+b_{t})$$

使用PyTorch构建模型：通过torch.nn.RNN可调用

# 导入工具包
>>> import torch
>>> import torch.nn as nn
>>> rnn = nn.RNN(5, 6, 1)
>>> input = torch.randn(1, 3, 5)
>>> h0 = torch.randn(1, 3, 6)
>>> output, hn = rnn(input, h0)
>>> output
tensor([[[ 0.4282, -0.8475, -0.0685, -0.4601, -0.8357,  0.1252],
         [ 0.5758, -0.2823,  0.4822, -0.4485, -0.7362,  0.0084],
         [ 0.9224, -0.7479, -0.3682, -0.5662, -0.9637,  0.4938]]],
       grad_fn=<StackBackward>)

>>> hn
tensor([[[ 0.4282, -0.8475, -0.0685, -0.4601, -0.8357,  0.1252],
         [ 0.5758, -0.2823,  0.4822, -0.4485, -0.7362,  0.0084],
         [ 0.9224, -0.7479, -0.3682, -0.5662, -0.9637,  0.4938]]],
       grad_fn=<StackBackward>)

input_size: 输入张量 $X$ 中特征维度的大小
hidden_size: 隐层张量 $h$ 中特征维度的大小
num_layers: 隐含层的数量
nonlinearity: 激活函数的选择, 默认是 $tanh$

传统RNN在解决长序列之间的关联时, 通过实践，证明经典RNN表现很差, 原因是在进行反向传播的时候, 过长的序列导致梯度的计算异常, 发生梯度消失或爆炸。

LSTM模型

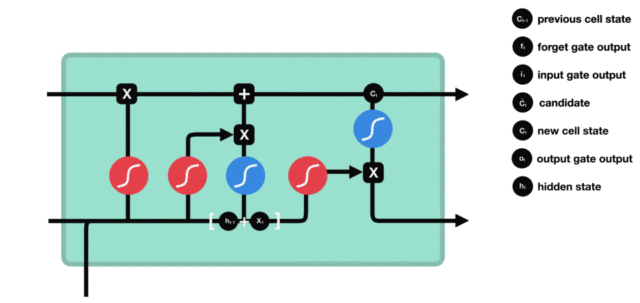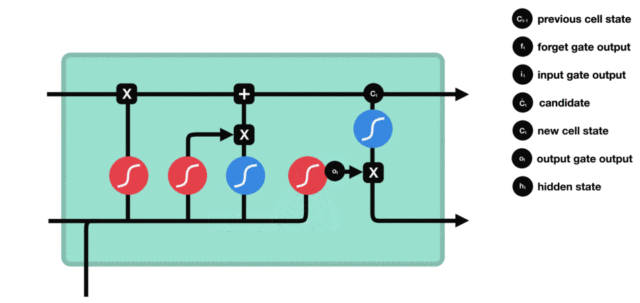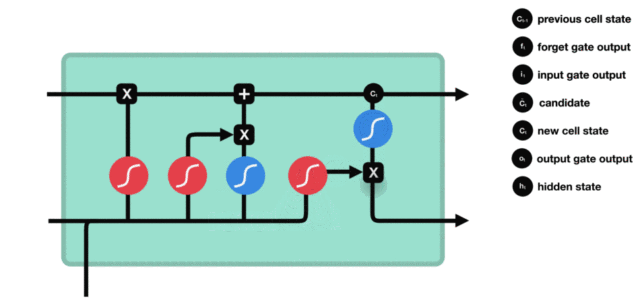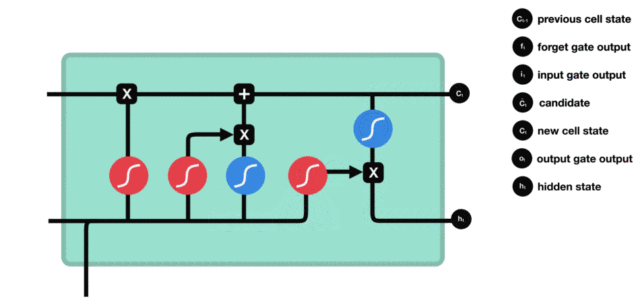
LSTM（Long Short-Term Memory）也称长短时记忆结构, 它是传统RNN的变体, 与经典RNN相比能够有效捕捉长序列之间的语义关联, 缓解梯度消失或爆炸现象. 同时LSTM的结构更复杂, 它的核心结构可以分为四个部分去解析:

遗忘门
输入门
细胞状态
输出门

遗忘门

与传统RNN的内部结构计算非常相似, 首先将当前时间步输入 $x(t)$ 与上一个时间步隐含状态 $h(t-1)$ 拼接, 得到 $[x(t), h(t-1)]$, 然后通过一个全连接层做变换, 最后通过 $sigmoid$ 函数进行激活得到 $f(t)$, 我们可以将 $f(t)$ 看作是门值, 好比一扇门开合的大小程度, 门值都将作用在通过该扇门的张量, 遗忘门门值将作用的上一层的细胞状态上, 代表遗忘过去的多少信息, 又因为遗忘门门值是由 $x(t), h(t-1)$ 计算得来的, 因此整个公式意味着根据当前时间步输入和上一个时间步隐含状态 $ h(t-1)$ 来决定遗忘多少上一层的细胞状态所携带的过往信息.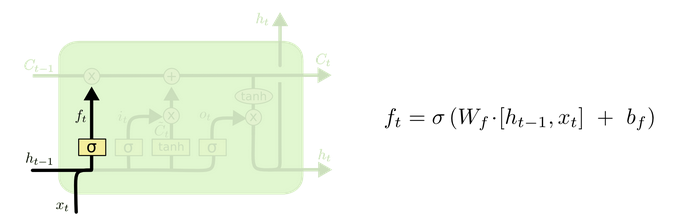

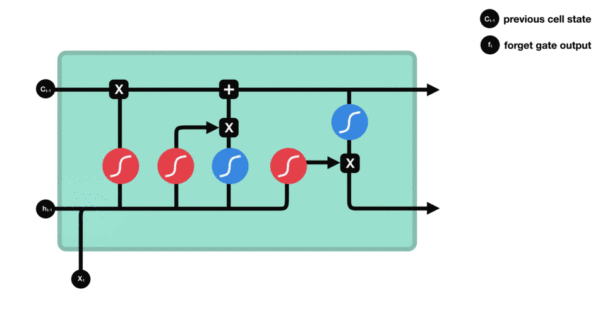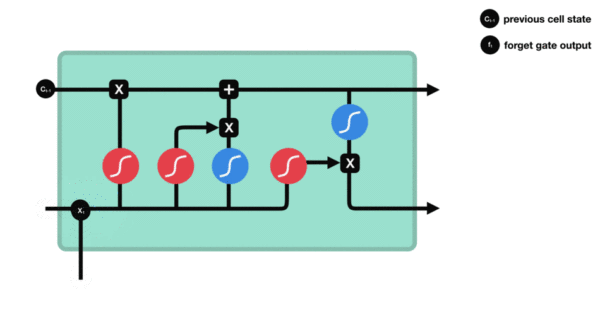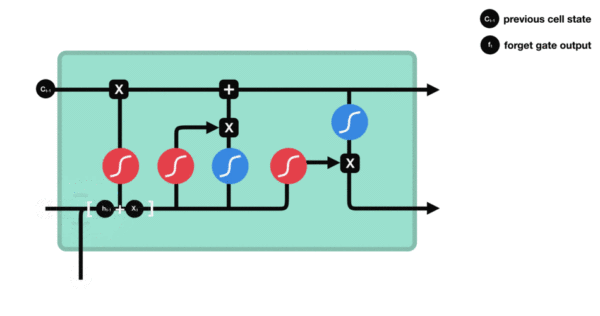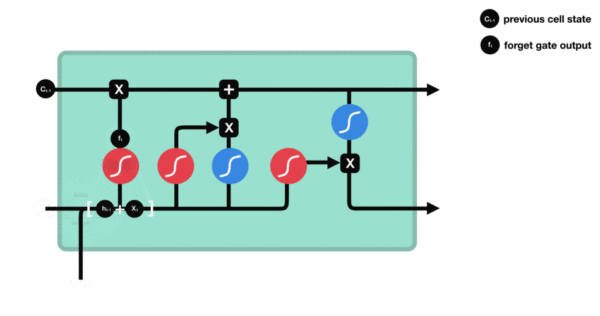
利用sigmoid函数将值压缩在0和1之间。

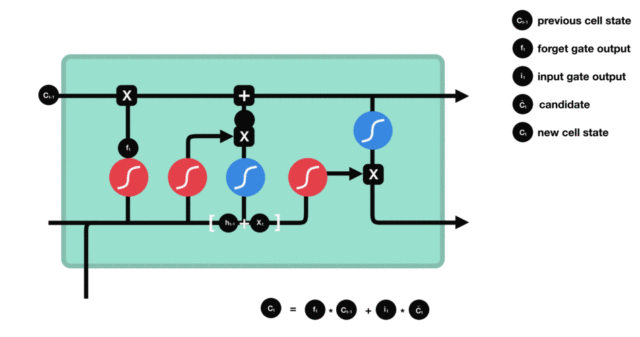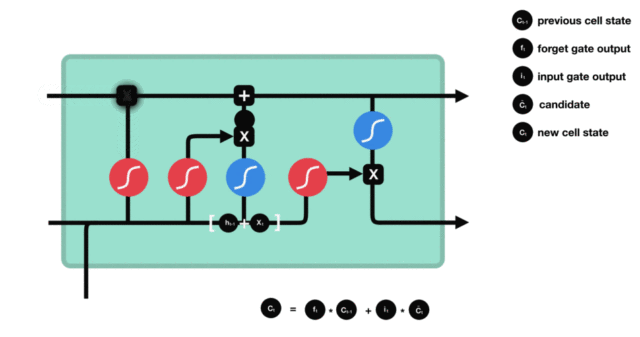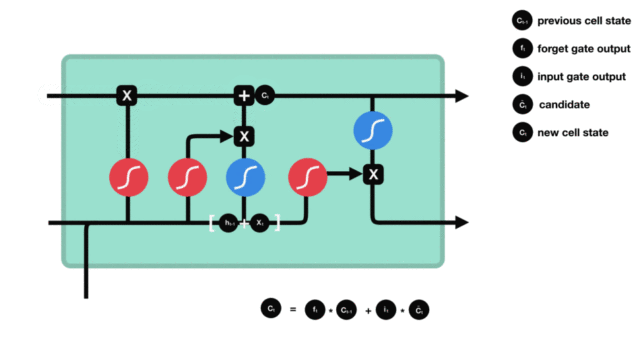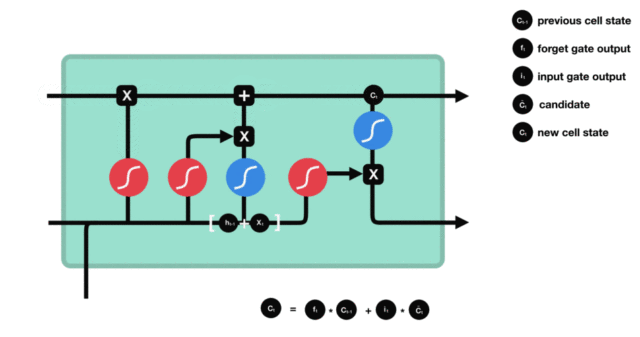
输入门和细胞状态

输入门的计算公式有两个, 第一个就是产生输入门门值的公式, 它和遗忘门公式几乎相同, 区别只是在于它们之后要作用的目标上. 这个公式意味着输入信息有多少需要进行过滤. 输入门的第二个公式是与传统RNN的内部结构计算相同. 对于LSTM来讲, 它得到的是当前的细胞状态, 而不是像经典RNN一样得到的是隐含状态.

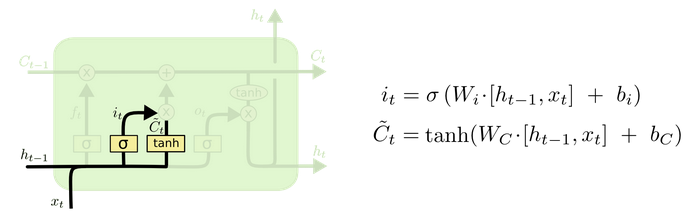
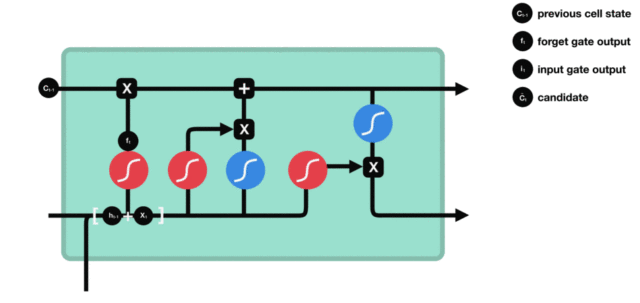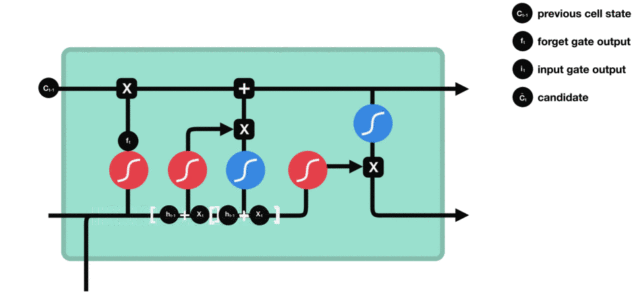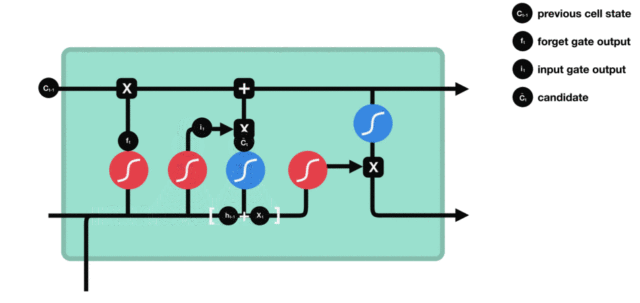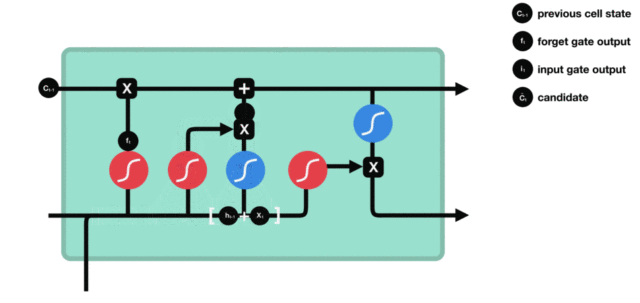
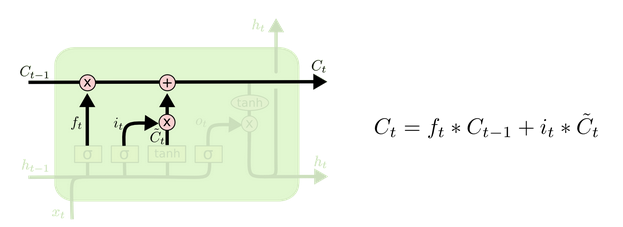
细胞更新的结构与计算公式非常容易理解, 这里没有全连接层, 只是将刚刚得到的遗忘门门值与上一个时间步得到的 $C(t-1)$ 相乘, 再加上输入门门值与当前时间步得到的未更新 $C(t)$ 相乘的结果. 最终得到更新后的 $C(t)$ 作为下一个时间步输入的一部分. 整个细胞状态更新过程就是对遗忘门和输入门的应用.

输出门

输出门部分的公式也是两个, 第一个即是计算输出门的门值, 它和遗忘门，输入门计算方式相同. 第二个即是使用这个门值产生隐含状态 $h(t)$, 他将作用在更新后的细胞状态 $C(t)$ 上, 并做 $tanh$ 激活, 最终得到 $h(t)$ 作为下一时间步输入的一部分. 整个输出门的过程, 就是为了产生隐含状态 $h(t)$ .

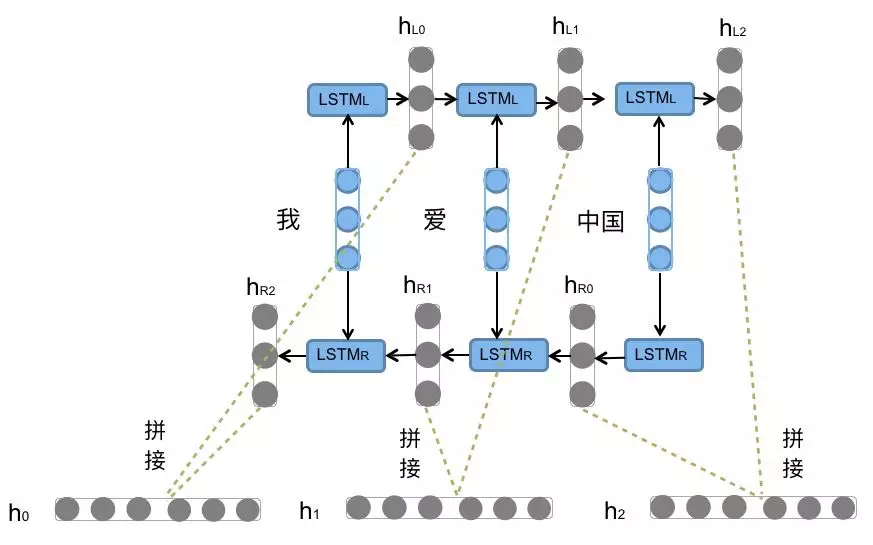
Bi-LSTM介绍

Bi-LSTM，即双向LSTM, 它没有改变LSTM本身任何的内部结构, 只是将LSTM应用两次且方向不同, 再将两次得到的LSTM结果进行拼接作为最终输出.

PyTorch构建LSTM模型：通过torch.nn.LSTM可调用。

# 定义LSTM的参数含义: (input_size, hidden_size, num_layers)
# 定义输入张量的参数含义: (sequence_length, batch_size, input_size)
# 定义隐藏层初始张量和细胞初始状态张量的参数含义:
# (num_layers * num_directions, batch_size, hidden_size)

>>> import torch.nn as nn
>>> import torch
>>> rnn = nn.LSTM(5, 6, 2)
>>> input = torch.randn(1, 3, 5)
>>> h0 = torch.randn(2, 3, 6)
>>> c0 = torch.randn(2, 3, 6)
>>> output, (hn, cn) = rnn(input, (h0, c0))
>>> output
tensor([[[ 0.0447, -0.0335,  0.1454,  0.0438,  0.0865,  0.0416],
         [ 0.0105,  0.1923,  0.5507, -0.1742,  0.1569, -0.0548],
         [-0.1186,  0.1835, -0.0022, -0.1388, -0.0877, -0.4007]]],
       grad_fn=<StackBackward>)
>>> hn
tensor([[[ 0.4647, -0.2364,  0.0645, -0.3996, -0.0500, -0.0152],
         [ 0.3852,  0.0704,  0.2103, -0.2524,  0.0243,  0.0477],
         [ 0.2571,  0.0608,  0.2322,  0.1815, -0.0513, -0.0291]],

        [[ 0.0447, -0.0335,  0.1454,  0.0438,  0.0865,  0.0416],
         [ 0.0105,  0.1923,  0.5507, -0.1742,  0.1569, -0.0548],
         [-0.1186,  0.1835, -0.0022, -0.1388, -0.0877, -0.4007]]],
       grad_fn=<StackBackward>)
>>> cn
tensor([[[ 0.8083, -0.5500,  0.1009, -0.5806, -0.0668, -0.1161],
         [ 0.7438,  0.0957,  0.5509, -0.7725,  0.0824,  0.0626],
         [ 0.3131,  0.0920,  0.8359,  0.9187, -0.4826, -0.0717]],

        [[ 0.1240, -0.0526,  0.3035,  0.1099,  0.5915,  0.0828],
         [ 0.0203,  0.8367,  0.9832, -0.4454,  0.3917, -0.1983],
         [-0.2976,  0.7764, -0.0074, -0.1965, -0.1343, -0.6683]]],
       grad_fn=<StackBackward>)

input_size: 输入张量x中特征维度的大小.
hidden_size: 隐层张量h中特征维度的大小.
num_layers: 隐含层的数量.
bidirectional: 是否选择使用双向LSTM, 如果为True, 则使用; 默认不使用.
input: 输入张量x.
h0: 初始化的隐层张量h.
c0: 初始化的细胞状态张量c.

由于内部结构相对较复杂, 因此训练效率在同等算力下较传统RNN低很多.

GRU模型

GRU（Gated Recurrent Unit）也称门控循环单元结构, 它也是传统RNN的变体, 同LSTM一样能够有效捕捉长序列之间的语义关联, 缓解梯度消失或爆炸现象. 同时它的结构和计算要比LSTM更简单, 它的核心结构可以分为两个部分去解析:

更新门
重置门

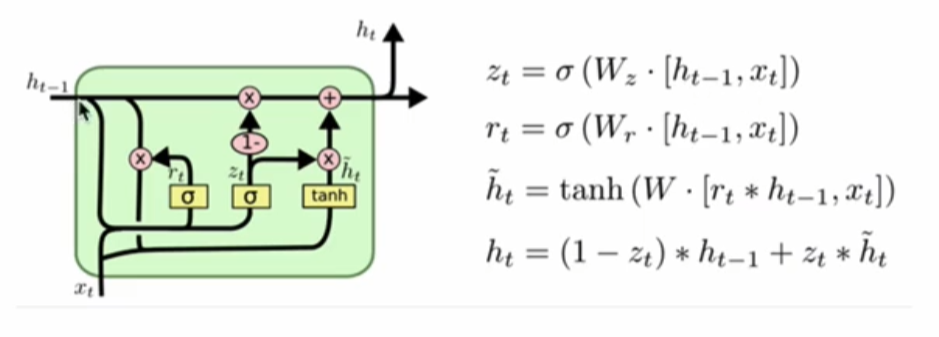
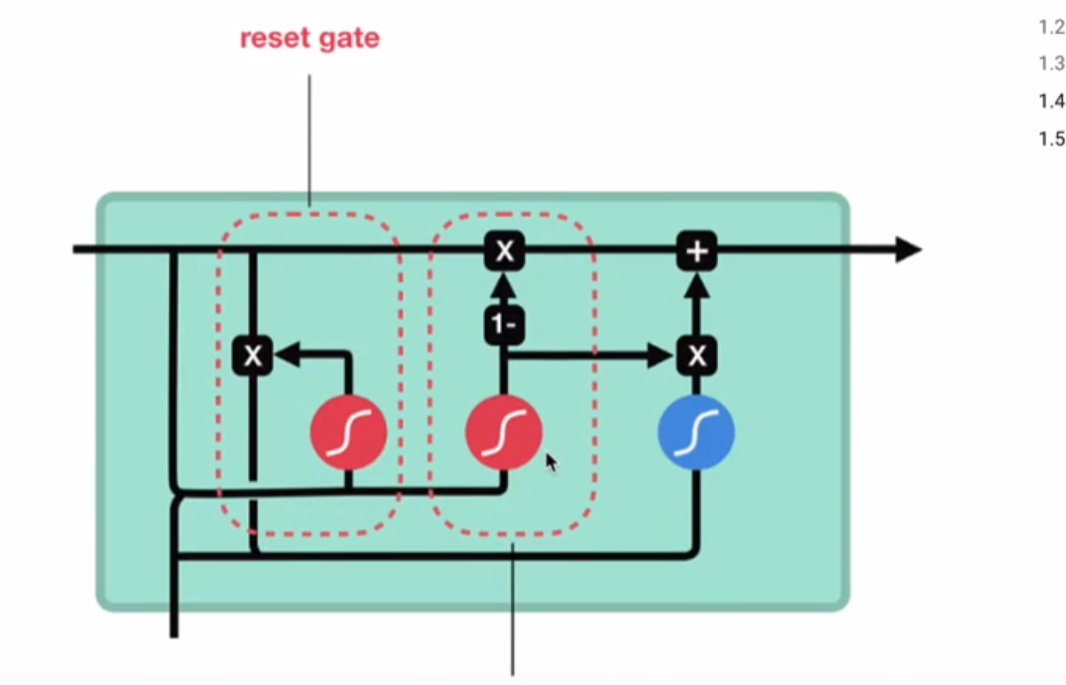
和之前分析过的LSTM中的门控一样, 首先计算更新门和重置门的门值, 分别是 $z(t)$ 和 $r(t)$
计算方法就是使用 $X(t)$ 与 $h(t-1)$ 拼接进行线性变换, 再经过sigmoid激活.
之后重置门门值作用在了 $h(t-1)$ 上, 代表控制上一时间步传来的信息有多少可以被利用.
接着就是使用这个重置后的 $h(t-1)$ 进行基本的RNN计算, 即与 $x(t)$ 拼接进行线性变化, 经过 $tanh$ 激活, 得到新的 $h(t)$ .
最后更新门的门值会作用在新的 $h(t)$ ，而 $1-$ 门值会作用在 $h(t-1)$ 上, 随后将两者的结果相加, 得到最终的隐含状态输出 $h(t)$ , 这个过程意味着更新门有能力保留之前的结果, 当门值趋于1时, 输出就是新的 $h(t)$ , 而当门值趋于0时, 输出就是上一时间步的 $h(t-1)$ .

使用Pytorch构建GRU模型：通过torch.nn.GRU可调用.

>>> import torch
>>> import torch.nn as nn
>>> rnn = nn.GRU(5, 6, 2)
>>> input = torch.randn(1, 3, 5)
>>> h0 = torch.randn(2, 3, 6)
>>> output, hn = rnn(input, h0)
>>> output
tensor([[[-0.2097, -2.2225,  0.6204, -0.1745, -0.1749, -0.0460],
         [-0.3820,  0.0465, -0.4798,  0.6837, -0.7894,  0.5173],
         [-0.0184, -0.2758,  1.2482,  0.5514, -0.9165, -0.6667]]],
       grad_fn=<StackBackward>)
>>> hn
tensor([[[ 0.6578, -0.4226, -0.2129, -0.3785,  0.5070,  0.4338],
         [-0.5072,  0.5948,  0.8083,  0.4618,  0.1629, -0.1591],
         [ 0.2430, -0.4981,  0.3846, -0.4252,  0.7191,  0.5420]],

        [[-0.2097, -2.2225,  0.6204, -0.1745, -0.1749, -0.0460],
         [-0.3820,  0.0465, -0.4798,  0.6837, -0.7894,  0.5173],
         [-0.0184, -0.2758,  1.2482,  0.5514, -0.9165, -0.6667]]],
       grad_fn=<StackBackward>)

GRU和LSTM作用相同, 在捕捉长序列语义关联时, 能有效抑制梯度消失或爆炸, 效果都优于传统RNN且计算复杂度相比LSTM要小.

但GRU仍然不能完全解决梯度消失问题, 同时其作用RNN的变体, 有着RNN结构本身的一大弊端, 即不可并行计算, 这在数据量和模型体量逐步增大的未来, 是RNN发展的关键瓶颈.

参考：

Deep Learning

RNN——循环神经网络

https://fabulous1496.github.io/2024/03/04/RNN/

作者

Fabulous

发布于

2024年3月4日

许可协议

Attention is all you need 上一篇

Fabulous の CS~61b 奇妙⭐冒险记下一篇