Fabulous の CS~61b 奇妙⭐冒险记
Testing
在工程中,为自己编写UnitTest时刻检测代码的正确性是十分重要且必要的。
假设我们现在有这样一个类,它实现对一个int类型的数组进行排序:
1 | |
我们可以编写一个SortTest类,来测试排序是否满足要求,假设我们要求将数组升序排序:
1 | |
这是一种近乎最原始的测试方式,但是可以直接有效的测试我们代码的可行性。
JUnit Testing
org.junit 库提供了许多有用的方法和有用的功能来简化测试的编写。例如,我们可以将上面的简单临时测试替换为:
1 | |
此方法测试 expected 和 actual 是否相等,如果不相等,则终止程序并显示详细错误消息。
Lists
The Mystery of the Walrus
现在有两段代码:
1 | |
对于第一段代码,我们输出结果能够发现a与b指向了同一个对象,而在第二段代码中,x和y却是不同的数值。
在java中,声明变量(基础类型的8种)并不会进行初始化。
这就意味着,如果有这样一行代码:
1 | |
如果不对x进行赋值,我们将无法使用变量x,即未完成实例化。
除开基础类型以外,其他的所有内容(包括数组)都不是原始类型,而是reference type。
当我们声明任何引用类型时,Java都会分配一个64bits的空间,无论对象是什么类型。
关键字new会将创建出的对象实例的地址传给左侧声明的对象。
赋值符号 “=” 表示将右侧变量的bits传给左侧对象。
1 | |
第一行表示声明一个Dog变量a,创建一个“10”的Dog实例并将其的地址传递给a,所以第二行表示将此实例的地址同样的拷贝传递给b,因此a和b实际上指向同一实例。
也就是说,对于基础类型,Java采用值传递的方式;而对于引用类型(reference type),Java采用引用传递的类型,这导致传递之后两个变量实际上指向同一个地址。
如上所述,储存数组的变量也是一种引用类型。
1 | |
第一行声明了一个int类型的数组x,但是并没有进行初始化,也就是说x内部为null。第二行则是创建了一个实例并将其绑定到数组x上,但是当第三行执行完毕后,我们将永远丢失数组{1, 2, 3}。
First taste of IntLists
我们可以尝试构建一个自己的int链表,包括获取大小、获取数据方法的实现(我最喜欢recursion了,我爱说实话):
1 | |
The SLList
在上面的链表实现中,用户可以直接看到内部的数据结构,这种 naked 的效果显然不是我们所期待的。
因此,我们将链表再次包装一层,避免裸露的数据结构,形成嵌套结构。
1 | |
之后,我们创建一个名为 SLList 的单独类,用户将与之交互。
1 | |
接下来是一些基础方法的实现,包括:addFirst, getFirst, addLast, size
1 | |
直观比较两个数据结构的区别:
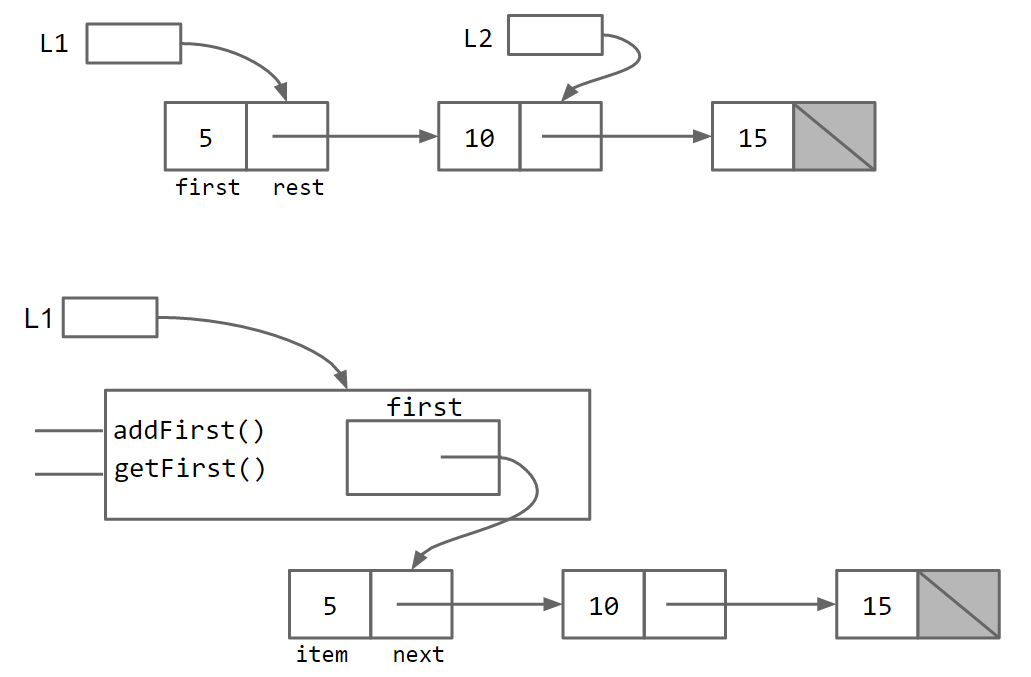
本质上,SLList 类充当列表用户和裸递归数据结构之间的中间人。正如上面在 IntList 版本中所建议的,IntList 用户可能拥有指向 IntList 中间的变量。进一步,我们还可以将属性改为private。
Nested Classes
对于SLList而言,IntNode是其中的嵌套类。
这种嵌套关系我们一般称之为 “has-a” 关系。
如果嵌套类不需要使用SLList的任何实例方法或变量,则可以声明为 static ,这意味着静态类中的方法无法访问封闭类的任何成员,节省内存。
Improvement
对 size() 方法进行分析,我们不难发现时间复杂度为 O(n) 。对于较大的列表来说,时间较长,所以我们考虑直接添加一个变量来跟踪当前链表的长度,这样时间复杂度变为了 *O(1)*。
1 | |
此外,我们发现初始创建空链表时,对其进行addLast方法会导致错误,这是因为 first 是 null ,因此尝试访问下面 while (p.next != null) 中的 p.next 会导致空指针异常。
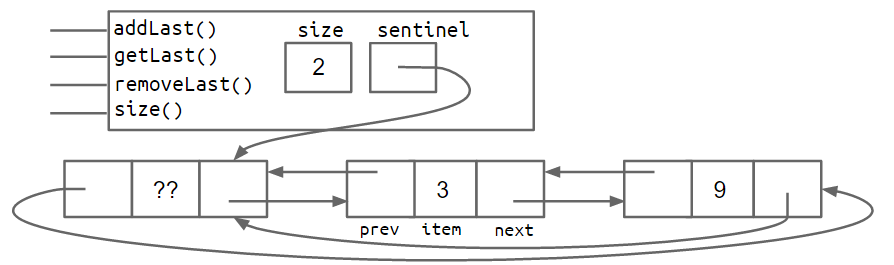
我们考虑加入不变的头节点(head),在此课程中称为 Sentinel Node 。
重构之后的代码:
1 | |
The DLList
对于SLList来说,向前搜索是十分困难的,当我们想获取最后一个节点时,不可避免的需要遍历整个链表。
因此我们考虑构造双向链表,每个节点都保存了前一个节点和后一个节点的信息。
主要有两种实现方式:循环链表(单个sentinel)和双向链表(双sentinel)。
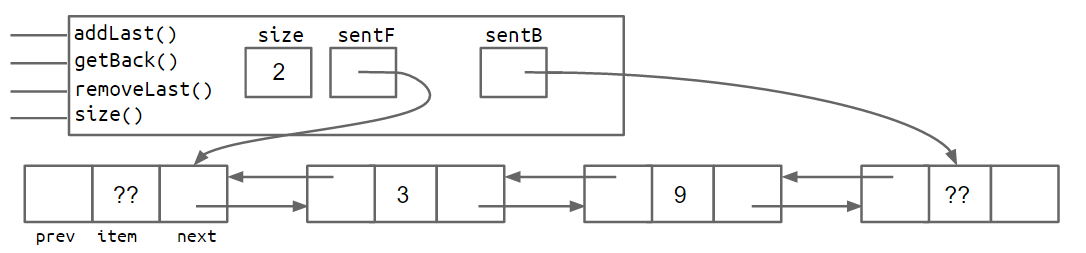
1 | |
First try of Generic Model
在Java中,我们可以通过泛型编程来实现对不同数据类型数据的存储。
基本语法是:在类声明中的类名之后,在尖括号内使用任意占位符 <> ,然后在任何使用任意类型的地方都使用该占位符。
1 | |
在实例化时,需要指明类型名。
1 | |
Arrays
创建数组有三种有效的方法
1 | |
Java中内置了一些与数组操作相关的方法
1 | |
在Java中,多维数组中的每个子数组可以有不同的长度。这种情况下,这些数组被称为不规则多维数组。Java中的多维数组实际上是数组的数组,因此每个子数组可以独立地具有不同的长度。
1 | |
The AList
对于链表来说,获取第i个节点元素需要从前向后遍历i次,这说明时间复杂度为 O(n) 。而在现代计算机上访问数组的第i个元素所需要的时间是恒定的,即 O(1) 。
A naive solution:
1 | |
对于这个方案,我们不难发现:数组的大小在一开始便固定下来了,这会导致我们在使用的过程中总会有空间浪费或空间不足的情况出现。
考虑性能,我们采用算法计算出最优化的数组大小并动态更新。
1 | |
Inheritance & Implements
Hypernyms, Hyponyms, and Interfaces Inheritance
具有 “is-a” 关系的词语之间互相为上位词与下位词。
例如:狗是贵宾犬、雪橇犬、哈士奇等的上位词。相反,贵宾犬、雪橇犬和哈士奇是狗的下位词。
换种说法,贵宾犬、雪橇犬、哈士奇都是狗的子类,而狗是贵宾犬、雪橇犬、哈士奇等的超类。
在Java中,为了表达这种层次结构,我们需要做两件事:
- 定义上位词的类型
- 指定下位词
我们定义出来的上位词类型便是所谓的接口(interface),它本质上只定义类所需要的功能,并不提供具体的实现方法,这一点可以看作C++中的抽象基类。
如果我们为之前创建的列表定义一个接口,那么应该是这样的:
1 | |
接下来,我们把AList和SLList指定为List61B的下位词,需要用到 implement 关键字:
1 | |
由于在接口中,我们仅仅声明了类中所包含的一些方法,并没有给出具体的实现过程,因此在子类中,我们需要对函数进行重写覆盖。在子类中实现所需的函数时,在方法签名的顶部包含 @Override 标记很有用。实际上,即使不包含标签,我们依旧在进行重写(Overriding)。
1 | |
和C++中一样,在Java中,接口类型的对象可以接受子类的对象。
1 | |
当它运行时,SLList 被创建,它的地址存储在 someList 变量中。然后字符串“elk”被插入到addFirst引用的SLList中。
在interface中,我们仅仅定义了方法头但并没有具体的实现。如果我们需要在接口中进行函数的实现并继承到子类中,我们可以在函数前加上 default 关键字。如果子类中没有重写,则会调用default方法,如果子类进行了重写,则会使用子类中的重写方法。
1 | |
Interface Inheritance vs Implementation Inheritance
- Interface Inheritance(接口继承):
接口继承是通过接口来定义的,一个接口可以扩展另一个接口。
通过接口继承,子接口可以继承父接口的抽象方法,但不继承任何具体的实现。
子接口可以定义新的抽象方法,或者通过默认方法提供方法的默认实现。
类实现一个接口时,必须提供接口中所有抽象方法的实现。
1 | |
- Implementation Inheritance(实现继承):
实现继承是通过类来定义的,一个类可以继承另一个类。
通过实现继承,子类继承了父类的所有属性和方法,包括具体的实现。
子类可以通过方法重写(override)来改变或扩展父类的方法的行为。
Java中一个类只能继承一个父类,即使是多重继承也只能通过接口实现。
1 | |
Externs, Casting, Higher Order Functions
我们使用 implements 关键字定义了类与接口之间的关系,对于类和类之间、接口与接口之间的继承关系,我们可以使用关键字 extends 进行定义。
1 | |
子类可以继承父类中的所有实例和静态变量,所有方法以及所有嵌套类。注意构造函数不是继承的,私有成员不能被子类直接访问。
虽然构造函数不是继承的,但 Java 要求所有构造函数都必须从调用其超类的构造函数之一开始。如果我们选择不这样做,Java 将自动为我们调用超类的无参构造函数。请注意,如果super class中的构造函数是有参的,那么要求在子类中显式地调用此构造函数。
1 | |
Java 中的每个类都是 Object 类或 extends Object 类的后代。即使类中没有显式 extends 的类仍然隐式扩展 Object 类。
Object 类提供了每个 Object 都应该能够执行的操作,例如 .equals(Object obj) 、 .hashCode() 和 toString() 。
有界类型参数:
在Java中,有界类型参数(bounded type parameters)是指在泛型类或泛型方法中对类型参数进行限制,使其必须是某种特定类型或其子类型。有界类型参数通常用于提高泛型的灵活性和安全性。
有界类型参数有两种:上界限定(upper bounded)和下界限定(lower bounded)。
- 上界限定:使用 extends 关键字指定类型参数必须是某个类或接口的子类。例如:
1 | |
在这个例子中,类型参数 T 必须是 Number 类或其子类,这意味着可以传递 Integer、Double、Float 等类型作为 T。
- 下界限定:使用 super 关键字指定类型参数必须是某个类的超类。例如:
1 | |
在这个例子中,类型参数 T 必须是 Number 类或其子类,这意味着可以传递 Integer、Double、Float 等类型作为 T。
Encapsulation
在编写代码的过程中,维持代码的 Abstraction Barriers 是非常重要的!(梦回61a)
在Java中,我们可以轻易地实现抽象障碍,比如使用private关键字。
但是继承可以破坏这种封装。
1 | |
前两个是基类,第三个则是子类中的部分。
调用子类中的函数,程序陷入无限循环。对 bark() 的调用将调用 barkMany(1) ,后者又调用 bark() ,无限次地重复该过程。
Casting
Java 有一种特殊的语法,您可以告诉编译器特定的表达式具有特定的编译时类型。
例如,我们有下面这个类:
1 | |
根据动态方法选择,调用dosomething时,检测到子类重写了这个方法,所以testa执行B中的dosomething函数。但编译器根据对象的静态类型确定某些内容是否有效,A中并没有donothing,所以会出错。
同样,func返回的是A类对象,不能用子类B类的对象直接接收。
我们使用casting解决。
1 | |
Higher Order Function
Python中,高阶函数是一个很有用的工具
1 | |
在Java中,我们可以利用接口继承实现高阶函数:
1 | |
有点类似于函数对象(谓词,伪函数)的实现。
Subtype Polymorphism
在Java中,多态性是指对象可以具有多种形式或类型。在OOP中,多态性涉及如何将对象视为其自身的实例、其超类的实例、其超类的超类的实例。
借由多态和接口继承,我们可以尝试实现运算符重载,尽管在Java中没有专门的操作。
1 | |
这样进行操作后,假设我们有其他类,也可以这样进行比较。如进行Dog和Cat之间的比较。
但是这样依然有缺陷,即强制类型转换时,可能会出错。这时我们考虑使用泛型。
java中已经为我们提供了接口 Comparable,故我们只需要实现
1 | |
Exceptions, Iterators, Object Methods
Lists, Sets, ArraySet
Java为我们提供了内置的List接口和多种实现,例如Arraylist。
1 | |
集合是唯一元素的集合,每个元素只能有一个副本,也没有顺序。Java 具有 Set 接口以及实现,例如 HashSet 。
1 | |
我们的目标是使用以下方法制作我们自己的集合 ArraySet :
add(value) :将值添加到集合中(如果尚不存在)
contains(value) :检查 ArraySet 是否包含该值
size() :返回大小
下面是一个框架:
1 | |
Throwing Exceptions
上面的框架中有一个错误,当我们将 null 添加到 ArraySet 时,我们会得到一个 NullPointerException。
问题在于 contains 方法,我们在其中检查 items[i].equals(x) 。如果 items[i] 处的值为 null,则我们将调用 null.equals(x) -> NullPointerException。
在Java中,我们使用关键字 throw 来抛出异常,语法格式:
1 | |
更新后的add方法:
1 | |
和C++一样,我们也可以使用try、catch 语句来进行异常的捕获(此处略)
Iteration
for each 循环:
1 | |
这种循环是将container中的每个object进入循环体中执行语句,支持这种循环的关键是迭代器。
在Java中,通过实现内置的 Iterable 接口,我们可以实现自己的迭代器。
1 | |
支持迭代器的 ArraySet 如下:
1 | |
Object Methods
所有类都继承自总体 Object 类。继承的方法如下:
1 | |
我们可以对这些方法进行重写。
Lecture 12 notes: Preview of Project 2
Command Line Compliation
The standard tools for executing java programs use to step process:
Hello.java ==> javac (Compiler) ==> Hello.class ==> java (Interpreter) ==> code
psvm
Java中的main函数的基本形式:
1 | |
其中,args储存了命令行参数。例如,我们有这样一个类:
1 | |
当我们在命令行内执行
1 | |
我们将会得到输出x y z。
Git:A Command Line Tool
git是一个用C语言编写的command line program
git提供了一个便捷的 Version Control 工具。
学习Git 找到一个网站:https://learngitbranching.js.org/?demo=&locale=zh_CN
当我们每次提交(commit changes)时,git都储存了一个整个repository的copy并保存在隐藏文件夹 .git 下。
我们假设一个程序员经历了下面三个步骤:
- V1:Create readme.md
- V2: Create some files, modify readme.md
- V3: Modify some files, change readme.md to V1 version
最自然的想法是在每次提交时都保存一份当前状态的副本,但是这种方法的缺点也是显而易见的。
稍加改进,我们发现每次提交时,并不是所有文件都会被修改,因此在下一次提交时,我们可以检查上一次保存的副本中是否含有相同的文件,并将本次保存的副本的相关文件用指针指向上一次的相同文件,这样就避免了同一份文件保存多次(指针只是形象的说明,Java没有指针 :P)。
在Java中,这种指向的一对一的键值对关系可以用map来保存。map的键为保存的文件,值记为版本号。
例如:
V1: X.java -> v1, Y.java -> v1
V2: X.java -> v1, Y.java -> v2
V3: X.java -> v1, Y.java -> v2, Z.java -> v3
V4: X.java -> v4, Y.java -> v2, Z.java -> v3, A.java -> v4
这表示在V4中,X.java使用v4当中修改的版本,Y.java使用v2中修改的版本,以此类推。在这里,我们保存的并不是文件的内容信息,而是“Y.java V4具有和V2相同内容”这一信息。
接下来我们考虑下面的情景:
A和B同时从V3开始修改,A修改了Horse.java 而B修改了Fish.java,两人都进行了提交,这时V4应该是什么呢?
为了解决这一问题,git中的版本号使用提交时间来定义,这大大降低了版本冲突的问题,但仍然存在多人同时提交的可能性。
所以git使用基于内容确定的SHA-1 hash值作为版本号,对于同一个值,对应的Hash值也相同,本质上是一个单值函数。
第一步,git计算出 SHA-1 hash值
Hello.java => 66ccdc645…
第二步,git创建一个文件夹,以前两个数字为标识
.git/objects/66
第三步,git储存内容在除去前两个数之后剩下部分(ccdc645…)命名的zlib文件中。
当文档的内容改变时,hash值也会改变,避免了版本名冲突。
每一个commit都包含了hash值、作者、时间和message。我们可以使用Serializable接口来实现对文件的操作。
在git中,我们拥有不同的分支以便储存不同的内容。在现实中,两个团队可能从同一个初始状态开始实现不同的功能,那么用不同的分支进行分隔是必要的。
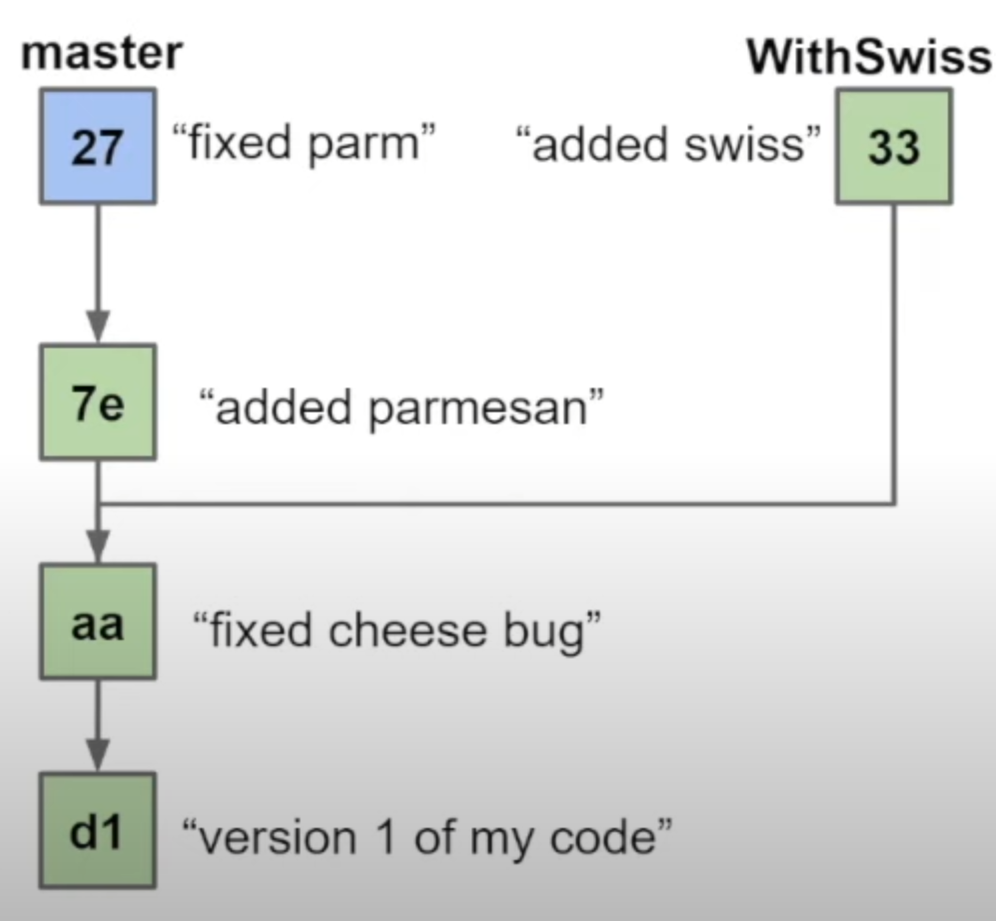
在完成之后,我们可以使用merge命令对分支进行合并。在这一过程中,我们用到了Graph的数据结构
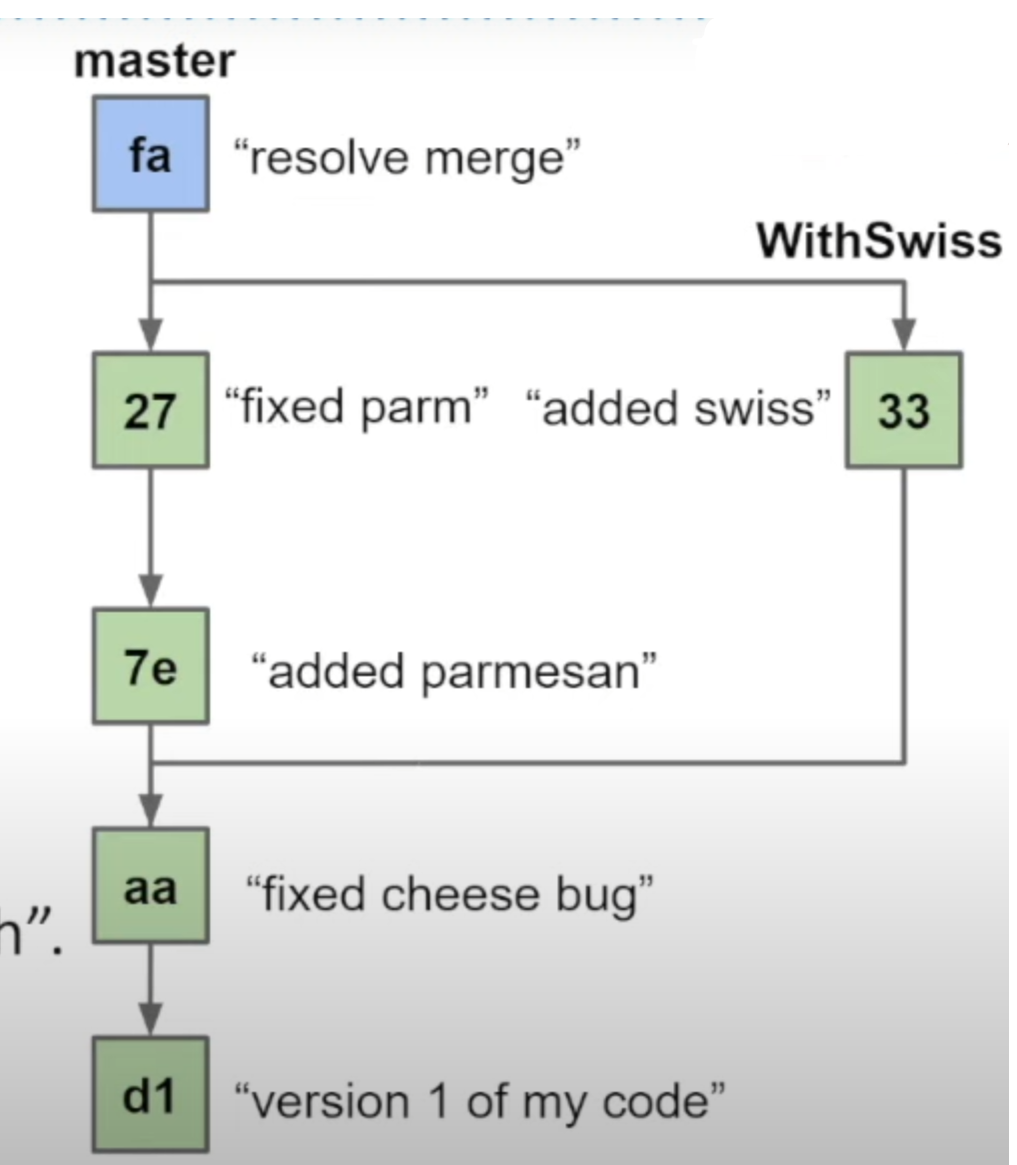
在git中,运用到了一些特殊的数据结构知识,下面是一个简短的preview
- Maps
- Hashing
- File I/O
- Graphs
File
使用File构造函数在Java中创造出一个File对象,并传入文件路径
1 | |
创建一个代表目录的File对象
1 | |
Serializable
实现Serializable接口的类表明它们可以被序列化,即可以将对象转换为字节序列,以便在网络上传输或保存到持久存储中,也可以将字节序列重新转换回对象。
1 | |
该接口没有方法;它只是为了一些特殊的 Java 类在对象上执行 I/O 的好处而标记其子类型。例如
1 | |
会将 m 转换为字节流并将其存储在名称存储在 saveFileName 中的文件中。然后可以使用诸如以下的代码序列来重建该对象:
1 | |
利用 utils.java 重写代码可以使代码更加简洁
1 | |
Efficient Programming
ADT
ADT(抽象数据结构)是由其行为而不是其实现定义的高级类型。
Proj1 中的 Deque 是一个具有某些行为(addFirst、addLast 等)的 ADT。但是,我们实际用来实现它的数据结构是 ArrayDeque 和 LinkedListDeque
- 数据封装: ADT 将数据和操作封装在一起,使得数据的内部结构对外部是不可见的。
- 操作定义: ADT 定义了数据类型支持的操作,并描述了这些操作的行为。
- 独立性: ADT 的实现可以独立于使用它的程序。
一些常用的 ADT 是:
Stacks:支持元素后进先出检索的结构
push(int x) :将 x 放入堆栈顶部
int pop() :取出栈顶元素Lists:一组有序的元素
add(int i) :添加一个元素
int get(int i) :获取索引 i 处的元素Sets:一组无序的唯一元素(无重复)
add(int i) :添加一个元素
contains(int i) :返回一个布尔值,表示集合是否包含该值Maps: 键/值对的集合
put(K key, V value) :将键值对放入映射中
V get(K key) :获取key对应的值
API
ADT 的 API(应用程序编程接口)是构造函数和方法的列表以及每个构造函数和方法的简短描述。
API由句法和语义规范组成。
- 规范性: API 提供了一组规范,定义了如何使用软件组件或服务。
- 抽象性: API 屏蔽了底层实现细节,使开发者可以专注于使用而不是实现细节。
- 互操作性: API 促进了不同软件系统之间的互操作性和集成。
Asymptotics
主要概念:
时间复杂度: 时间复杂度描述了算法执行所需时间与输入规模之间的关系。通常以大 O 表示法来表示,表示算法的渐进上界。例如,如果一个算法的时间复杂度为 O(n),则表示算法的运行时间与输入规模成线性关系。
空间复杂度: 空间复杂度描述了算法在执行过程中所需的内存空间与输入规模之间的关系。也通常以大 O 表示法来表示。
渐进分析: 渐进分析是指对算法性能进行预测时,主要考虑随着输入规模的增长,算法的运行时间或空间占用的变化趋势。在这种分析中,我们更关注算法的增长率而不是确切的运行时间或空间。
最坏情况复杂度: 最坏情况复杂度描述了算法在最坏情况下的时间或空间开销。这给出了算法性能的一个保证,即算法在任何情况下都不会比最坏情况更差。
平均情况复杂度: 平均情况复杂度描述了算法在平均情况下的时间或空间开销。这需要考虑所有可能输入的概率分布,并计算平均性能。
最优算法: 最优算法是指在给定问题上具有最低时间复杂度或空间复杂度的算法。找到最优算法通常是解决特定问题的目标之一。
这章主要介绍了时间复杂度和空间复杂度的计算,以及一些经典算法的时间复杂度分析方法,如小o、大O法等,此处不再举例说明。
Disjoint Sets
不相交集的定义:如果两个集合没有共同元素,则它们被称为不相交集合。该数据结构有两个操作:
- connect(x, y):连接x和y,也被称为union
- isConnected(x, y):返回x和y是否连接
不相交集数据结构具有固定数量的元素,每个元素都从自己的子集中开始。通过对某些元素 x 和 y 调用 connect(x, y) ,我们将子集合并在一起。
1 | |
Quick Find
直观上,我们可能首先考虑将不相交集表示为集合列表:
[{0}, {1}, {2}, {3}, {4}, {5}, {6}]
但这样如果我们进行connect操作,需要遍历List,时间复杂度为 $O(n)$ 。
所以我们考虑使用数组表示:
- 数组的索引代表我们集合的元素。
- 索引处的值是它所属的集合编号。
例如,我们将 {0, 1, 2, 4}, {3, 5}, {6} 表示为:

执行connect操作就是把对应序号的值改为集合的编号
执行isConnected操作即检查序号的值是否相等。
1 | |
Quick Union
在Quick Find中,如果我们想要快速的将多个集合connect是非常困难的。
这时,我们考虑为每个项目分配其父集的索引编号而不是id,如果一个集合没有父项,我们为其赋值为-1.
这种方法支持我们将每个集合想象成一棵树。例如,我们将 {0, 1, 2, 4}, {3, 5}, {6} 表示为:

对于 QuickUnion,我们定义了一个辅助函数 find(int item) ,它返回 item 所在树的根。例如,对于上面的集合, find(4) == 0 、 find(1) == 0 、 find(5) == 3 等。每个元素都有一个唯一的root.
当我们想要连接两个集合时,我们只需要将A集的root连接到B集的root上,即把A集作为B集的一个branch。
检查两个集合是否为相连的,我们只需要检查两个集合是否具有相同的root。
在性能方面,利用树可以使连接变得十分简单,但相应的,当我们想要查找某一个元素时,我们需要遍历树的各个branch,时间复杂度为 $O(n)$
1 | |
Weighted Quick Union (WQU)
Quick Union 的改进依赖于一个关键的思路:每当我们调用 find 时,我们都必须找到树的根部。因此,树越短,速度就越快。
所以在我们将两个树相连时,我们选择将较小的树作为子树连接到较大的树上。
如何衡量树的大小?在这里,我们用树包含的元素的数量作为树的Weight。
基于这种方法,我们所获得的树的最大高度将会为 $logN$ ,其中 $N$ 为树所包含元素的数量。
我们假设有树 $T_{1},T_{2}$ ,其中 $T_{1}$ 包含了元素 $x$ , $size(T_{2}) \ge size(T_{1})$ 。当我们合并两个tree时,我们将 $T_{1}$ 连接到 $T_{2}$ 下,这个操作使 $x$ 的深度增加1,而整个合并的树大小至少为 $T_{1}$ 的两倍,也就是说 $2^{h} = N$ ,最大高度 $h = \log_{2}{N}$
Weighted Quick Union with Path Compression
在上面的方法中,每次我们调用 find(x) 时,我们必须遍历从x到root 的路径,因此在这个过程中,我们可以将访问的所有项目连接到它们的root,无需额外的渐进成本。
这称为摊销运行时间,我们通过这种方式使树变得更短。
Binary Search Trees
Now we are going to learn about perhaps the most important data structure ever. –Josh Hug, CS61b
对于搜索项目而言,有序数据结构如链表一般效率较高。但即使是已排序的列表,对于搜索项目的时间复杂度依旧为 $O(n)$ 。
对于数组,我们可以使用二分查找来更快的找到元素。
Binary Search
使用二分查找的条件:
- 数据结构必须是有序的
- 访问数据结构的任何元素都需要恒定时间
二分查找的一般步骤:
在二分查找算法中,通过查找中间索引 “mid” 将搜索空间分为两半
如果mid不是我们需要的,选择元素存在的一侧继续进行二分查找,知道找到或者空间耗尽。
1 | |
基于有序链表,我们实现BST的步骤一般如下:
- 将哨兵节点指向链表的中间,并更改链表之间的指向
- 判断要搜索的元素位于哪一侧
- 在一侧递归上述过程
Tree
下面我们给出严格的树定义。
树由节点以及连接节点的这些边组成。
注意:任意两个节点之间有且仅有一条路径,即不形成回路,没有连支。
没有父节点的节点称为root,根节点。在拓扑学中,根节点实际上存在多种可能性,这里我们只任意选取一种。
没有子节点的节点称为叶子(leaf)
将其与我们之前提出的原始树结构联系起来,我们现在可以向已经存在的约束引入新的约束。这会创建更具体类型的树。
- Binary Trees:二叉树,规定每个节点最多只有2个子节点
- Binary Search Trees
二叉搜索树,是一种二叉树,对于树中的每个节点X:
- 左子树中的每个键都小于X的键
- 右子树中的每个键都大于X的键
基于这种特殊的性质,我们得以将二分搜索应用于这种数据结构上。
对于二叉搜索树的插入操作,我们基于以下的思路:
- 首先我们搜索该节点,如果该节点已经存在,则不需要插入
- 如果我们没有找到该节点,实际上我们停止搜索的位置正好就是应该插入的位置的父节点,此时我们可以将新的leaf添加到节点的左侧或右侧。
对于二叉树的删除方法,我们需要考虑三种情况:
- 删除一片叶子
- 删除一个有一个子节点的节点d
- 删除一个有两个子节点的节点
对于叶子,我们直接删除父节点和叶子之间的边即可
对于一个子节点,我们只需要将该节点的父节点的指针指向该节点的子节点即可
对于两个子节点,我们用右子树最左侧的节点(最小值)代替删除的节点或用左子树最右侧的节点(最大值)代替该节点。
一个简单的实现:
1 | |
Tree traversal
对于树,我们有这样四种遍历的方式
- 前序遍历(根优先遍历,即对于每个树和子树,按照根-左树-右树的顺序遍历)
- 中序遍历(左树-根-右树)
- 后序遍历(左树-右树-根)
- 层次遍历(具有相同深度的称为一层)
这里我们实现中序遍历:
我们在迭代器中使用一个栈来辅助遍历。在将元素压入栈中的过程中,我们需要注意以下几点:
找到左子树的最左节点:首先,我们需要找到当前节点的左子树的最左节点。这个节点是中序遍历中的第一个要访问的节点。
将节点压入栈中:一旦找到了左子树的最左节点,我们将该节点压入栈中。
更新当前节点:然后,我们将当前节点移动到其右子树。如果右子树不为空,我们继续重复步骤 1 和 2。
重复直到完成:我们重复执行上述步骤,直到栈为空。当栈为空时,说明 BST 中的所有节点都已经遍历完成。
下面是一个例子:
1 | |
首先,我们将根节点 5 压入栈中,并且将根节点的左子树全部压入栈中,直到左子树的最左节点 2。此时,栈中的元素为 [2, 3, 5]。
接着,我们开始执行迭代器的 next() 方法。在 next() 方法中,我们首先弹出栈顶节点 2,然后将其右子节点 null 压入栈中。此时,栈中的元素为 [3, 5]。
继续执行 next() 方法,我们弹出栈顶节点 3,返回 3。然后,将其右子节点 4 压入栈中。此时,栈中的元素为 [4, 5]。
再次执行 next() 方法,我们弹出栈顶节点 4,返回 4。此时,栈中的元素为 [5]。
继续执行 next() 方法,我们弹出栈顶节点 5,返回 5。然后,将其右子节点 8 压入栈中,并将右子树的所有左子节点全部压入栈中,直到左子树的最左节点 7。此时,栈中的元素为 [7, 8]。
继续执行 next() 方法,我们弹出栈顶节点 7,返回 7。然后,将其右子节点 null 压入栈中。此时,栈中的元素为 [8]。
最后,我们弹出栈顶节点 8,返回 8。然后,将其右子节点 9 压入栈中,并且将右子节点的所有左子节点全部压入栈中,直到左子树的最左节点 9。此时,栈中的元素为 [9]。
最终,我们执行 next() 方法,弹出栈顶节点 9,返回 9。此时,栈为空,遍历结束。
通过这个过程,我们按照中序遍历的顺序遍历了二叉搜索树中的所有节点,迭代器的 next() 方法成功返回了所有节点的键值。
Tree Height
在最好情况下,search操作的时间为 $\Theta (\log{}{N})$ ,但最差情况下可以达到 $\Theta (n)$ 。
- depth: 节点与根之间的链接数
- height: 树的最低深度(深度最大)
- average depth:平均深度
树的高度决定了最坏情况下的运行时间,因为在最坏情况下我们需要的节点在树的底部。
平均深度决定了平均运行时间。
B-Trees
当我们插入新数据时,我们总是会将新数据插入到原来的叶子上,这样便造成了树的高度增加。更严重的是,当我们的数据呈现出连续的特点时,我们会沿着一条路线不断向下,导致整棵树的结构试去平衡,也使算法效率降低。
于是我们便有了这样一个想法:当我们添加节点时,永远不要添加叶节点,而是将原有的叶节点扩充,即一个节点依次存放多于一个数据。
这样做的确使结构平衡,减小了高度,但是在新添加的数据量级较大时,并没有降低复杂度。
于是我们将添加的数据继续分离,将中间的一部分沿树枝向上添加到父节点中,使得整个树更加平衡。这样,对于每一个节点,我们都可以拥有含有两个元素的子节点,并保持节点之间的有序排列,这便是B树的定义。
我们主要讨论 2-3 树,即一个节点可以最多包含两个元素,三个子节点。
B树的主要特点包括:
- 每个节点最多有m个子节点。
- 除了根节点和叶节点外,每个节点至少有⌈m/2⌉个子节点。
- 根节点至少有两个子节点,除非它是一个叶节点。
- 所有叶节点都出现在同一层级。
- 一个非叶节点如果有k个子节点,那么它包含k-1个键。每个内部节点的键作为分隔值,将其子树分开。
B-Tree Deletion
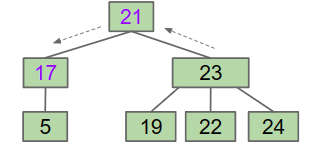
CASE1:邻近的兄弟节点有多个Key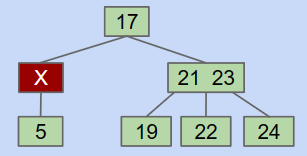
这种情况下,我们用父节点填充删除节点,用邻近兄弟节点的较小Key填充父节点.
CASE2:父节点含有两个Key,邻近的兄弟节点只有一个。
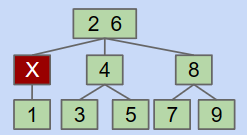
在这种情况下,父节点的左值分配到左孩子,右值分配到右孩子,中间的子节点的两个孙节点分别分配到其余节点下。
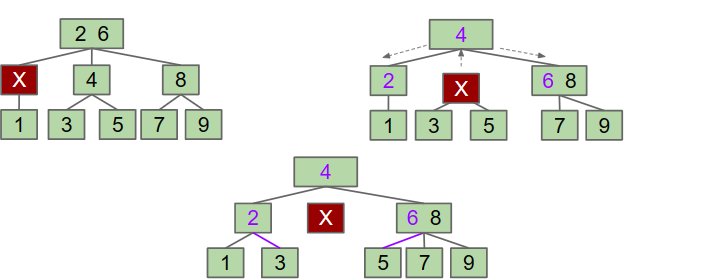
CASE3:父节点和邻近兄弟节点均只有一个Key
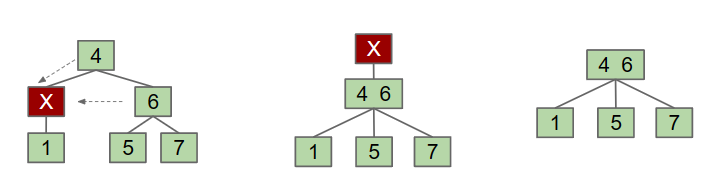
Tree Rotation
在上面的算法中,我们多次用到了CASE1中类似于“旋转”的操作。接下来我们就来正式的定义这种操作并用算法实现。
The formal definition of rotation is:
1 | |
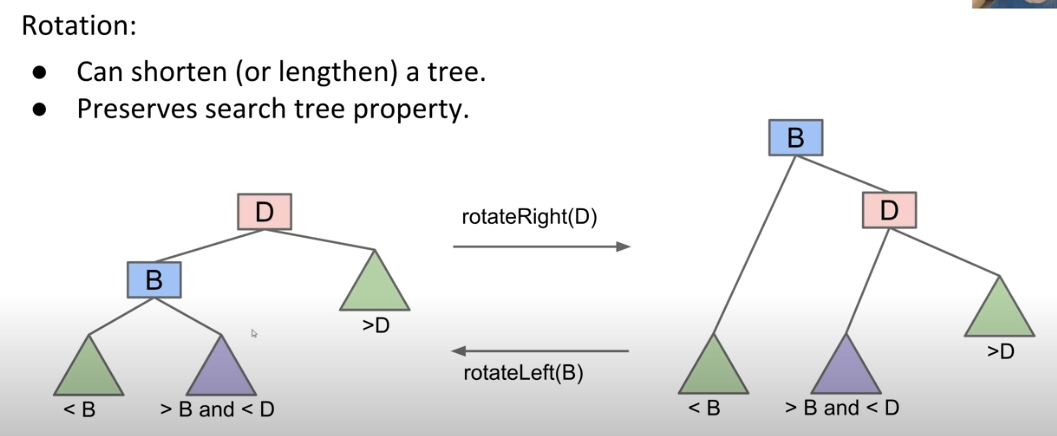
通过基础的旋转操作,我们可以实现简单的节点重构。
Red-Black Tree
2-3 树的想法非常好,但实际上很难实现,于是我们考虑创建一种同时使用BST和2-3树的结构的新的树。
我们首先考虑如何将2-3树转换为BST。
对于只有两个子节点的2-3树,我们已经有了BST结构,因此不需要进行修改;但是对于有三个子节点的树,我们首先要做的便是创建一个“粘合节点”,它不保存任何信息,仅用于表明它的两个子节点实际上时一个节点的一部分。
然而,这是一个非常不优雅的解决方案,因为我们占用了更多的空间,而且代码也很难看。因此,我们将使用粘合链接而不是使用粘合节点!
我们选择使左侧元素成为右侧元素的子元素。这会产生一棵左倾树。我们通过将链接设为红色来表明它是粘合链接。正常链接是黑色的。因此,我们将这些结构称为左倾红黑树(LLRB)。
2-3树和LLRB之间存在一一对应的双射关系。
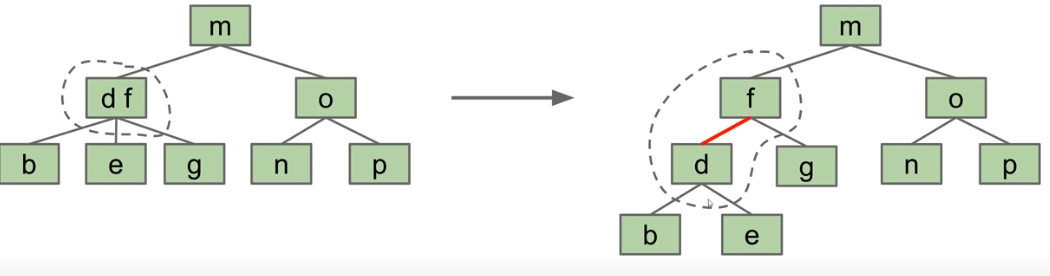
注意:要构成有效的红黑树,需要满足以下条件:
- 每个节点只能有不多于一个红色链接
- 每条从leaf 到 root 的路径具有相同的黑色链接数量。
- 若原本2-3树的高度为 $H$ ,LLRB的高度不超过 $2H+1$ 。
Tree Insertion
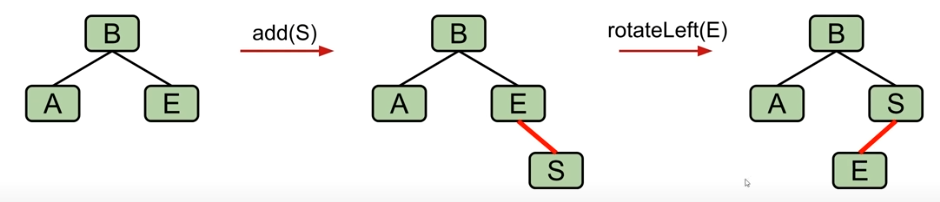
向红黑树中插入节点,需要解决以下几个问题:
- 插入的颜色:在2-3树中,我们总是通过添加到叶节点来插入,所以我们添加的链接应该是红色链接。

- 插入方向:我们使用的是LLRB,这意味着我们永远不可能拥有右侧的红色链接,如果需要在右侧插入,我们需要进行必要的旋转操作。
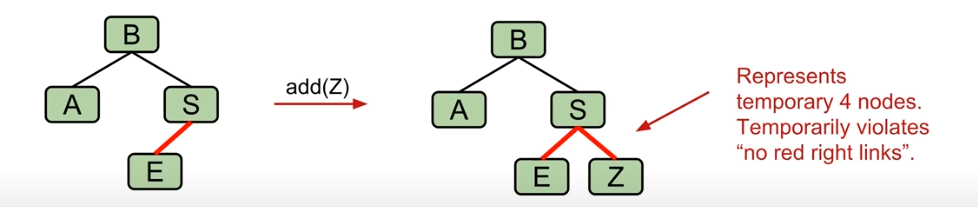
- 引入暂时的 4节点 解决问题
之后我们利用 flip 操作来进行规范化操作。

抽象代码:
1 | |
Hashing
DataIndexedIntegerSet
对于我们已经学习到的数据结构,我们需要寻找某一元素时,都需要遍历整个结构。这样通常会花费 $O(n)$ 运行时甚至更多。于是我们考虑设计这样一个数据结构,让寻找元素的时间变为 $O(1)$ 。
于是我们考虑这样一种数据结构:我们创建一个非常大的数组,存放boolean类型的数据,将数组的 index 作为数据的值。初始时我们将元素设置为false,代表没有存放对应序号的数据。在添加数据时,只需要将对应位置的元素更改为true即可。这样,我们的search和contains操作都将是 $O(1)$ 复杂度。
1 | |
显然,这个数据结构占用空间大、存储数据类型单一、浪费资源,但是却为我们提供了一个很好的思路。
DataIndexedStringSet
接下来我们尝试在数据结构中插入String类型的数据。
基于上面的思想,我们也考虑使用一个算法将每一个String转化成唯一的一个Integer。比如我们为每一个英文字母和符号分配一个数值,用数值加和得出的结果来代表这个单词。
这里很自然的我们想到利用ASCII码来处理。
在算法方面,我们考虑借鉴进制的定义,比如十进制利用0到9的十个数字表示出所有自然数。我们以 126 为基,这样 “cat” 便可以表示为:
$$cat = char(c)\times 126^{2}+char(a)\times 126^{1}+char(t)\times 126^{0}$$
其中char代表对应的ASCII码值。
这样,我们便可以使用int代替String,接下来就可以用int进行存储。
但是,如果我们想要储存中文,最大的可能符号有 40959 种,意味着我们需要一个大于39万亿的数组存储,这显然是不现实的!
Hash Code
对于小范围的哈希值,我们可以使用一个数组来区分每个哈希值。也就是说,数组中的每个索引都代表一个唯一的哈希值。如果我们的指数很小并且接近于零,那么这种方法很有效。
假设我们只想支持长度为 10 的数组,以避免分配过多的内存。此时,我们可以依靠取模运算实现这一点。
所以要创建有效的哈希码,我们需要考虑下述维度:
- Deterministic:确定性,两个相等的对象 A 和 B ( A.equals(B) == true ) 的 hashCode() 函数具有相同的哈希码。
- Consistent:每次在对象的同一实例上调用 hashCode() 函数时,它都会返回相同的整数。
在此基础上,如果需要拥有高效的哈希码,我们需要进一步考虑以下问题:
- hashCode() 函数必须有效。
- hashCode() 函数值应尽可能均匀地分布在所有整数的集合上。
- hashCode() 函数的计算速度应该相对较快[理想情况下为 $O(1)$ 常数时间数学运算]
由于数据溢出等特殊情况,出现冲突是不可避免的。对于这种情况,我们有以下方式进行处理:
线性探测:将冲突键存储在数组中的其他位置,可能存储在下一个开放数组空间中。这种方法可以通过分布式哈希表看到。
外部链接:一个更简单的解决方案是将具有相同哈希值的所有键一起存储在它们自己的集合中,例如 LinkedList 。这种共享单个索引的条目集合称为存储桶。
对于哈希表,一旦表中数据越来越倾向于饱和,发生冲突和错误的可能性就越大。因此,动态调整哈希表的大小是十分必要的。
为了跟踪哈希表的填充程度,我们定义了术语负载因子,它是插入的元素数量与数组总物理长度的比率。
$$load \ factor=\frac{size()}{array.length}$$
对于我们的哈希表,我们将定义允许的最大负载因子。如果添加另一个键值对会导致负载因子超过指定的最大负载因子,则应调整哈希表的大小。这通常是通过将基础数组长度加倍来完成的。 Java 默认的最大负载因子是 0.75,它在合理大小的数组和减少冲突之间提供了良好的平衡。
Heaps and Priority Queues
在二叉搜索树BST中,我们能够高效地搜索到需要的元素,只需要 $\log{}{N}$ 的时间复杂度。如果我们更加关心快速找到最小或最大元素而不是快速搜索怎么办?
Priority Queue
我们先来看优先队列的接口:在我们定义的最小优先队列中,我们只能与队列中的最小元素进行交互。
1 | |
我们考虑使用已经学习过的数据结构进行实现:
- Ordered Array 有序数组
- BST 二叉搜索树
- HashTable 哈希表
Heaps
经过比较,我们发现BST具有已知的最佳运行效率。我们考虑在BST的基础上继续进行改进,可以进一步提高这些操作的运行时间效率。
我们定义 Heap 的数据结构,这是一种完全二叉树,即具有:
- 堆序性质(Heap Property):在堆中,对于每个节点 i,父节点的键值小于或等于(小顶堆)或大于或等于(大顶堆)其子节点的键值。
- 完全二叉树结构(Complete Binary Tree Structure):堆是一种完全二叉树,即除了最底层节点,其他层的节点都是满的,最底层节点都尽可能地靠左排列。
堆分为两种类型:最小堆和最大堆。在最小堆中,父节点的键值始终小于或等于其子节点的键值;而在最大堆中,父节点的键值始终大于或等于其子节点的键值。
Java实现最小优先队列的示例代码:
1 | |
如果不调用封装好的类,我们可以用计数器的思想实现优先级。即:计数器在每次插入项目时都会递增。最近插入的项目始终具有更高的优先级,因此它们将首先被删除。
一个可能的示例:
1 | |
一般而言,Heap有如下的性质使得它能很方便地实现优先队列的数据结构:
高效的插入和删除操作:堆的插入和删除操作的时间复杂度为 $O(log n)$ ,其中n是堆中元素的数量。这使得堆非常适合用于实现优先队列,因为在优先队列中,我们经常需要插入和删除元素。
快速访问最小(或最大)元素:堆允许在常数时间内 $O(1)$ 访问堆顶元素,这是因为堆的根节点始终是最小(或最大)的元素。这对于优先队列来说非常重要,因为我们经常需要知道当前队列中优先级最高的元素。
自动维护顺序:堆具有自我调整的性质,即在插入或删除元素后,堆会自动调整其结构以保持堆的性质。这意味着我们不需要手动维护堆的顺序,从而简化了代码实现。
支持动态大小:堆可以动态地调整大小,因此可以容纳任意数量的元素。这使得堆非常适合用于实现优先队列,因为我们通常不知道在队列中需要存储多少元素。
一些有意思的点:
按降序排序的数组是最大堆(根是最大值,值按级别顺序递减)。
Graph
一般来说,图由两部分组成:
- 一组节点
- 一组边,有向或无向
所有树也是图,但并非所有图都是树。
对于图,我们一般考虑下列问题:
- 路径:顶点 s 和 t 之间是否存在路径?
- 连通性:图是否连通,即所有顶点之间是否存在路径?
- 双连通性:是否存在删除某个顶点会断开图的连接?
- 最短 s-t 路径:顶点 s 和 t 之间的最短路径是多少?
- 环路检测:图表中是否存在环路?
- 同构:两个图是否同构(同构图)?
总体来说,最根本的还是一个问题:我们如何遍历图?
Graph traversal
我们先关注第一个问题:如何确定两个节点 $s$ 和 $t$ 之间是否存在路径.
我们考虑一个函数:它接受两个顶点并返回两者之间是否存在路径。实现这个函数,我们可以以第一个节点为参考节点,然后访问他的一个邻居节点并将自己标记为已查找。之后对第二个节点递归的调用该函数知道找到目标节点或遍历完整个路径(所有节点均被标记)。
具体而言,可以拆解为以下步骤:
- 从图中的某个顶点开始遍历,将该顶点标记为已访问。
- 递归地对该顶点的未访问邻居顶点进行深度优先遍历。
- 重复步骤2,直到该顶点的所有邻居顶点都被访问过。
- 回溯到上一个顶点,重复步骤2和步骤3,直到图中的所有顶点都被访问过。
事实上,这正是图的深度优先遍历算法(Depth-First Search,DFS)。我们可以尝试用伪代码来实现一下:
1 | |
我们也可以用栈来优化递归操作,在这里不做展示。
深度优先遍历算法的时间复杂度为 $O(V + E)$ ,其中 $V$ 是顶点的数量,$E$ 是边的数量。
事实上,我们也能用另一种思路解决这个问题:
我们先将第一个节点的所有邻居访问完成,然后逐层向下地访问其它节点。这一思想称为广度优先搜索(Breadth-First Search,BFS)。我们一般使用队列来进行实现:
- 在遍历的过程中,先将起始顶点加入队列,然后重复以下步骤直到队列为空
- 弹出队列中的顶点,并访问该顶点。
- 遍历该顶点的所有邻居顶点,如果某个邻居顶点未被访问过,则将其加入队列,并标记为已访问。
1 | |
Graph Representing
表示图的方式有很多,常见的是用邻接矩阵(Adjacency Matrix)和邻接表(Adjacency Lists)。
Adjacency Matrix
使用二维数组。有一条边将顶点 s 连接到 t ,前提是相应的单元格是 1 (表示 true )。请注意,如果图是无向的,则邻接矩阵将在其对角线上(从左上角到右下角)对称。
Adjacency Lists
维护一个列表数组,按顶点号索引。如果存在从 s 到 t 的边,则数组索引 s 处的列表将包含 t 。
Shortest Paths–Dijkstra’s Algorithm
Dijkstra算法是计算机科学中的一种流行算法,用于在图中找到节点之间的最短路径,特别是在具有非负边权重的图中。
该算法通过迭代地选择从源节点开始的已知距离最小的节点,并在发现更短路径时更新其相邻节点的距离来运作。它通过维护一个优先队列(通常用最小堆实现)来高效地选择下一个要探索的节点。
以下是Dijkstra算法的步骤概述:
初始化: 将源节点的距离设置为0,将所有其他节点的距离设置为无穷大。初始化一个空的优先队列(或最小堆),用于按距离排序的节点。
选择下一个节点: 从优先队列中提取具有最小距离的节点。最初,这将是源节点。
更新相邻节点: 对于当前节点的每个相邻节点,计算通过当前节点到源节点的距离。如果此距离比先前已知的距离更短,则更新相邻节点的距离并更新其父节点(找到最短路径的节点)。将更新后的相邻节点插入优先队列。
重复: 重复步骤2和3,直到所有节点都被处理或达到目标节点。
最短路径重建: 一旦到达目标节点或所有节点都已处理,就可以通过在算法执行过程中存储的父指针回溯从目标节点到源节点,重建从源到目标的最短路径。
下面是一个可能的伪代码实现:
1 | |
Minimum Spanning Trees
最小生成树(Minimum Spanning Tree,MST)是一种在连通加权图中找到的特殊树形结构,它包含了图中的所有顶点,并且是一个树,没有环路,同时权重之和最小。
割集(Cut Set)是指一个图中的边集合,当这些边被移除后,原本连通的图被分割成两个或多个不相连的子图。换句话说,割集是一组边,它们的移除会使得图中的顶点失去连接,导致图分裂成多个连通分量。
连支(Connected Components)是指图中的一组顶点,它们之间有路径相连,并且没有其他的顶点与这些顶点相连。连支是由顶点组成的集合,用于描述图的连通性。
寻找连通图的最小生成树,一般而言有两种算法,均基于贪心思想:
- Kruskal 算法
- Prim 算法
时间复杂度均为 $O(E\log{}{V})$ 。
Prim’s Algorithm
基本思想:
Prim 算法也是一种贪心策略,从一个初始顶点开始,逐步扩展最小生成树,每次选择与当前最小生成树相连的权重最小的边,并且不会形成环路。
Prim 算法在稠密图中效果更好,适用于边的数量与顶点数量相当的情况。
步骤:
- 选择一个起始顶点作为初始树。
- 将与初始树相连的边加入候选边集合中。
- 从候选边集合中选择权重最小的边,将其加入最小生成树,并将其所连接的顶点加入最小生成树的顶点集合中。
- 重复步骤3,直到最小生成树包含了图中的所有顶点。
Kruskal’s Algorithm
基本思想:
Kruskal 算法基于贪心策略,每次选择权重最小的边,如果这条边不形成环路,则将其加入最小生成树。
Kruskal 算法对于稀疏图效果较好,适用于边的数量远远大于顶点数量的情况。
步骤:
- 将图中的所有边按照权重从小到大排序。
- 依次从排序后的边集合中选取边,如果选取的边不会形成环路(即加入这条边后不会出现环路),则将其加入最小生成树。
- 重复步骤2,直到最小生成树中包含了图中的所有顶点为止。
Mutidimensional Data
对于一维数据的存储,我们有十分简便的比较大小的方式。但是对于二维乃至于多维的数据,如果我们想要分类,一个依据是每个维度进行大小的比较,这时候就需要增加树的节点个数来表示不同的区间。
Quadtree
四叉树(Quadtree)是一种用于表示二维空间的树形数据结构,它将二维空间递归地划分为四个象限,每个象限可以继续划分为四个子象限,以此类推。四叉树常用于表示和管理二维数据。
- 空间划分:四叉树将二维空间划分为四个象限:左上、右上、左下、右下。每个象限可以继续划分为四个子象限,以此类推,直到达到某个终止条件。
- 节点结构:四叉树的节点包含四个指针,分别指向其四个子节点。如果一个节点没有子节点,则称为叶子节点。叶子节点通常包含相应区域内的数据。
- 查询操作:四叉树可以快速进行区域查询和范围查询。区域查询用于查找落在给定区域内的所有数据点,而范围查询用于查找与给定点距离不超过一定范围内的所有数据点。
- 空间分析:四叉树可以用于进行空间分析,如判断两个区域是否相交、计算区域的面积、查找最近邻点等。
K-D Trees
KD 树(K-Dimensional Tree)是一种二叉树数据结构,用于对 k 维空间中的数据进行分割和组织。KD 树常被用于对多维数据进行搜索、范围查询和最近邻搜索等操作。
- 空间划分:KD 树通过递归地将 k 维空间划分为轴对齐的超矩形区域。每个节点代表一个超矩形区域,其子节点对应于该区域被分割后的子区域。
- 轴选择:在构建 KD 树时,每次选择一个坐标轴作为切分的依据。通常,轴的选择是交替进行的,比如在二维空间中就是交替选择 x 轴和 y 轴。
- 节点结构:KD 树的节点包含一个数据点以及指向左右子节点的指针。根据选择的切分轴,左子节点的数据点在该轴上小于当前节点的值,右子节点的数据点在该轴上大于当前节点的值。
- 搜索操作:KD 树可以用于范围查询和最近邻搜索。范围查询用于查找落在给定超矩形区域内的所有数据点,最近邻搜索用于查找离给定点最近的数据点。
构建 KD 树的步骤:
- 选择初始轴(通常是坐标轴)。
- 根据选定的轴,找到中位数,将数据集分为两部分。
- 递归地构建左右子树,重复步骤 1 和步骤 2,直到每个区域只包含一个数据点为止。
最近邻搜索算法(Nearest Neighbor Search):
1 | |
Prefix Operations and Tire
前缀操作(Prefix operation)是一种数学和计算机科学中的操作符表示法,其中运算符位于其操作数之前。这种表示法也称为波兰记法或前缀表示法。在前缀表示法中,运算符位于操作数之前,这与我们通常使用的中缀表示法(如2 + 3)或后缀表示法(逆波兰表示法,如2 3 +)不同。
例如,常见的算术表达式“2 + 3”在前缀表示法中将写为“+ 2 3”。在这个例子中,“+”是运算符,而“2”和“3”是操作数。
前缀表示法具有几个优点:
- 无需括号:由于运算符位于操作数之前,不需要使用括号来表示优先级。
- 易于计算:计算机在处理前缀表示法时通常使用栈来进行计算,这使得计算过程更加简洁和高效。
- 易于转换:前缀表示法可以很容易地转换为后缀表示法或中缀表示法,从而便于人们阅读和理解。
对于前缀操作,我们可以使用Tire树进行相关操作。
Tire Tree
Trie树(也称为前缀树或字典树)是一种树形数据结构,用于存储动态集合,其中键通常是字符串。Trie树的名称来源于”retrieval”,表明其主要用途是支持快速的检索操作。
在Trie树中,每个节点代表一个字符,通常从根节点开始,到达每个节点的路径表示从根到该节点的字符序列。叶节点通常表示一个完整的单词,但也可能只是一个前缀。
一个简单实现:
1 | |
为了让Tire能够高效地进行前缀匹配操作,我们可以定义一些方法:
首先我们考虑定义一个 collect 方法,该方法可以用于返回Tire中的所有键。
伪代码:
1 | |
基于 collect 方法,我们可以定义 keyWithPrefix 方法,返回具有特定前缀的所有键。
1 | |
DAG and Topological Sorting
拓扑排序(Topological Sorting)是一种用于有向图的排序算法,它能够将图中的节点按照它们之间的依赖关系进行排序,使得所有的依赖关系都得到满足。
在拓扑排序中,如果存在一条从节点 A 到节点 B 的路径,那么在排序结果中节点 A 将位于节点 B 之前。换句话说,所有的依赖关系都是从左到右的。
拓扑排序通常应用于有向无环图(DAG),因为有向无环图是一种没有循环依赖的图,可以通过拓扑排序进行有效的排序。
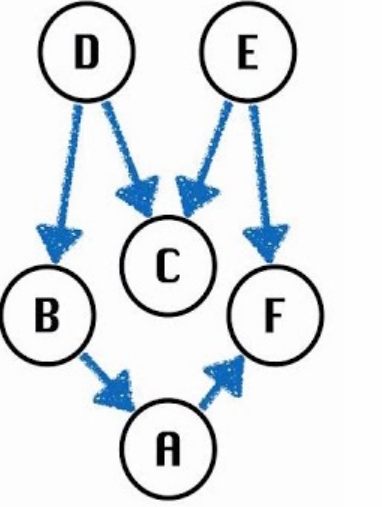
对于上图中的DAG,我们有这样的一些有效的拓扑排序:
- $[D, B, A, E, C, F]$
- $[E, D, C, B, A, F]$
对于任何拓扑排序,我们都可以重绘图形使每个顶点都位于一条直线上,这称为图的线性化。
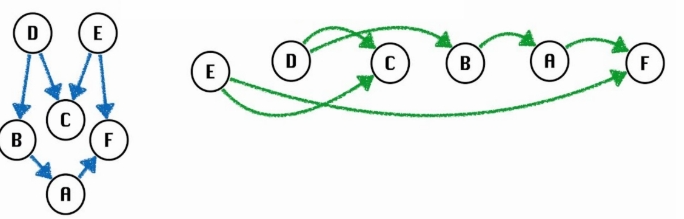
Topological Sort Algorithm
我们一般利用DFS(深度优先搜索)来实现对DAG的拓扑排序。
- 对于有向图中的每个节点,初始化一个标记数组,用于标记节点是否被访问过,以及一个栈或者列表用于存储排序结果。
- 从图中任意未被访问的节点开始,对每个未被访问的节点执行步骤 3。
- 对于当前节点,进行深度优先搜索:
- 将当前节点标记为已访问。
- 对当前节点的所有邻居节点(即当前节点指向的节点)进行递归调用步骤 3。
- 将当前节点压入栈或者添加到列表中。
- 当对当前节点的所有邻居节点都完成了深度优先搜索后,返回到步骤 2,选择另一个未被访问的节点进行深度优先搜索。
- 当所有节点都被访问并完成深度优先搜索后,栈或列表中的顺序就是拓扑排序的结果。
利用python实现:
1 | |
Shortest Paths on DAGs
Dijkstra算法可以计算最短路径,但是在边的权重为负值时,算法无法保证有效性。
我们考虑使用拓扑排序加动态规划的思想,对Dijkstra算法进行补全。
下面给出一个可能的步骤:
- 对 DAG 进行拓扑排序,得到节点的拓扑排序顺序。
- 初始化一个距离数组,用于存储从起始节点到每个节点的最短距离。将起始节点的距离设为 0,其他节点的距离设为正无穷大。
- 按照拓扑排序的顺序依次处理每个节点:
- 对于当前节点 u,遍历其所有的邻居节点 v。
- 对于每个邻居节点 v,更新其距离为 min(当前距离[v], 当前距离[u] + 边(u, v)的权重)。
- 最终,距离数组中存储的就是从起始节点到每个节点的最短路径长度。
Sorts
在最后,我们了解并实践一些常见的排序算法。
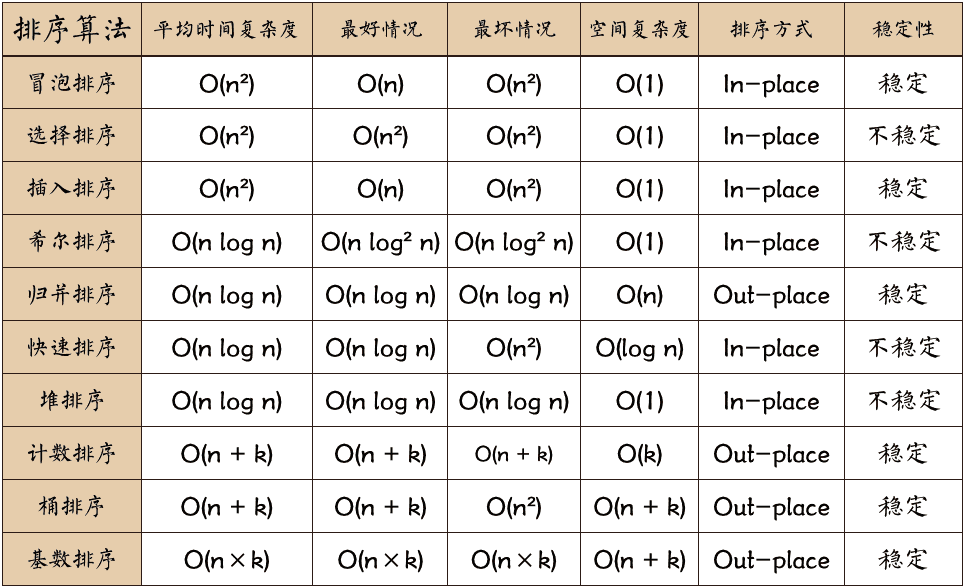
Bubble Sort
冒泡排序(Bubble Sort)也是一种简单直观的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢”浮”到数列的顶端。
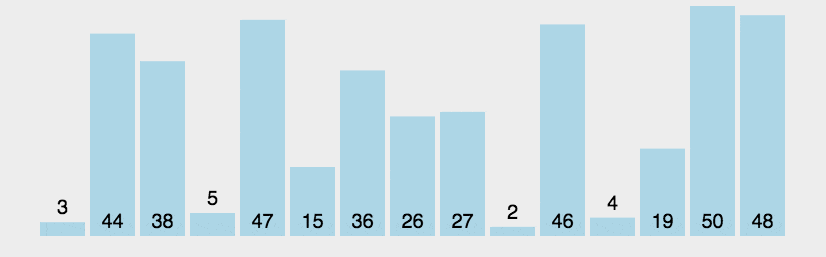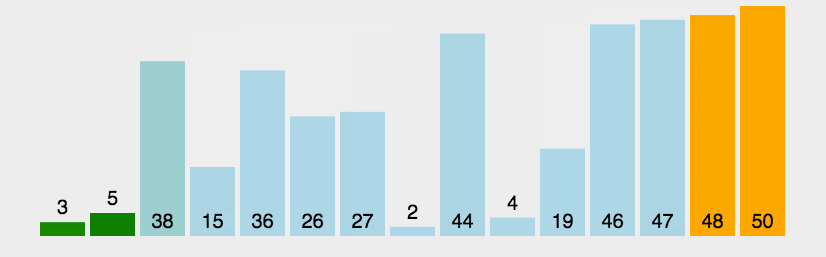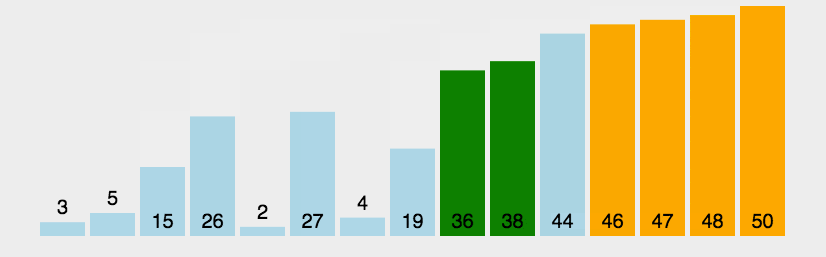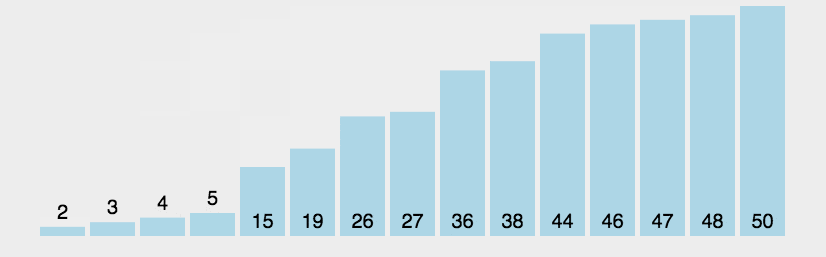
1 | |
Select Sort
选择排序的基本思想:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕。
1 | |
Insert Sort
插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
1 | |
Shell Sort
希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录”基本有序”时,再对全体记录进行依次直接插入排序。
1 | |
Merge Sort
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
1 | |
Heap Sort
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法:
- 大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列;
- 小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列;
堆排序的平均时间复杂度为 Ο(nlogn)。

1 | |
Quick Sort
快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下,排序 n 个项目要 Ο(nlogn) 次比较。在最坏状况下则需要 Ο(n2) 次比较,但这种状况并不常见。事实上,快速排序通常明显比其他 Ο(nlogn) 算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来。
快速排序使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。
快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看,快速排序应该算是在冒泡排序基础上的递归分治法。
算法步骤:
从数列中挑出一个元素,称为 “基准”(pivot);
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
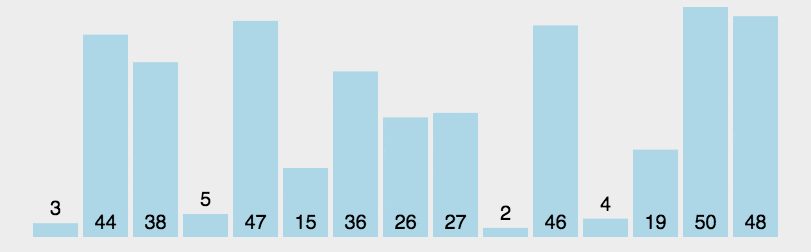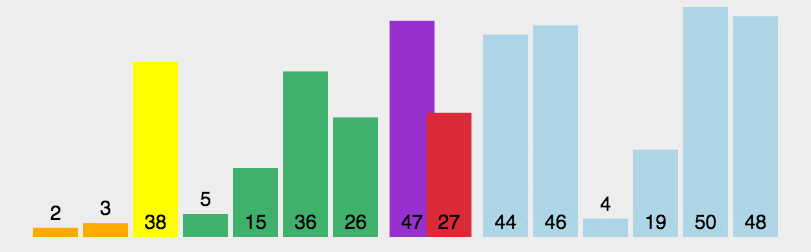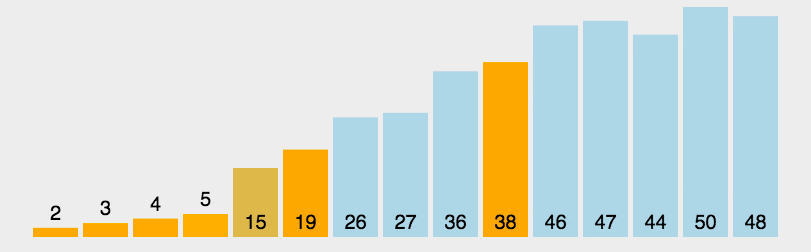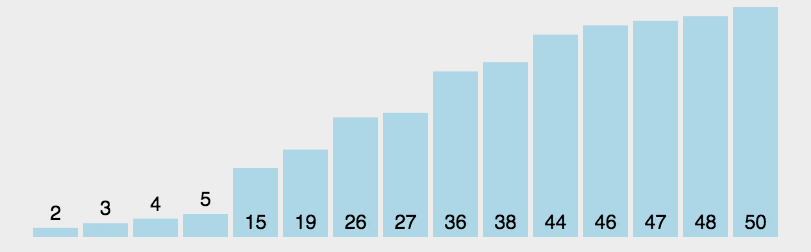
1 | |
Counting sort
计数排序(Counting Sort)是一种非比较型的整数排序算法,它利用输入数据的特定范围进行排序。计数排序的基本思想是统计每个输入元素的出现次数,然后根据元素的值和出现次数,将元素放置到正确的位置上。
以一个例子说明:
假设我们有一个待排序的整数数组 [4, 2, 2, 8, 3, 3, 1]。
确定输入数据的范围(最大值和最小值)。在这个例子中,最大值是 8,最小值是 1。
创建计数数组,并统计每个元素的出现次数。
元素 出现次数 1 1 2 2 3 2 4 1 5 0 6 0 7 0 8 1 将计数数组转换为每个元素在输出数组中的起始位置。
元素 出现次数 起始位置 1 1 0 2 2 1 3 2 3 4 1 5 5 0 6 6 0 6 7 0 6 8 1 7 创建输出数组,并将待排序数组中的元素放置到输出数组的正确位置上。
- 从待排序数组的最后一个元素开始遍历,即
arr = [4, 2, 2, 8, 3, 3, 1]。 - 当前元素是 1,在计数数组中的起始位置是 0,因此放置到输出数组的索引位置为 0。
- 当前元素是 3,在计数数组中的起始位置是 3,因此放置到输出数组的索引位置为 3。
- 当前元素是 3,在计数数组中的起始位置是 3,因此放置到输出数组的索引位置为 4。
- 依此类推,将所有元素放置到输出数组的正确位置上。
- 从待排序数组的最后一个元素开始遍历,即
输出数组即为排序后的结果。在这个例子中,排序后的数组是
[1, 2, 2, 3, 3, 4, 8]。
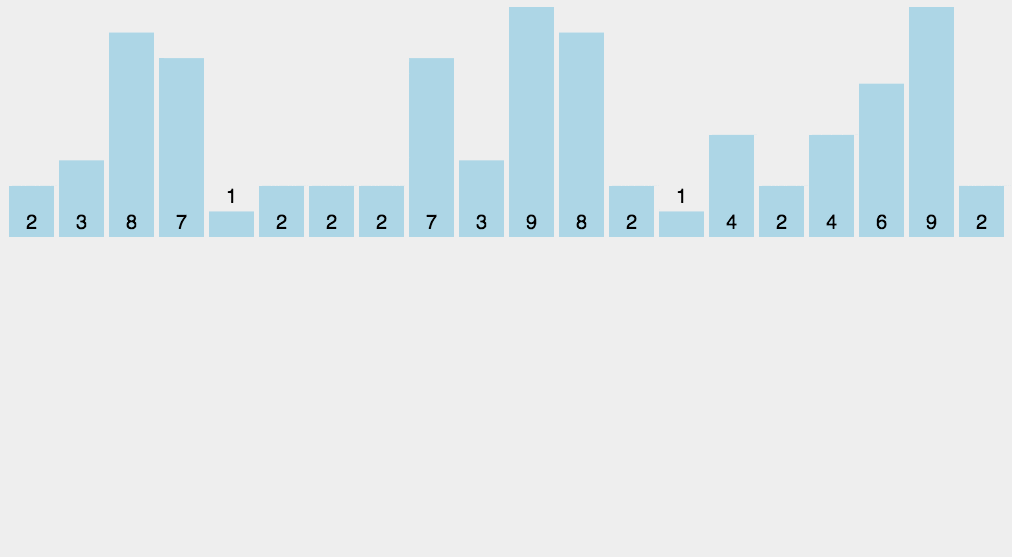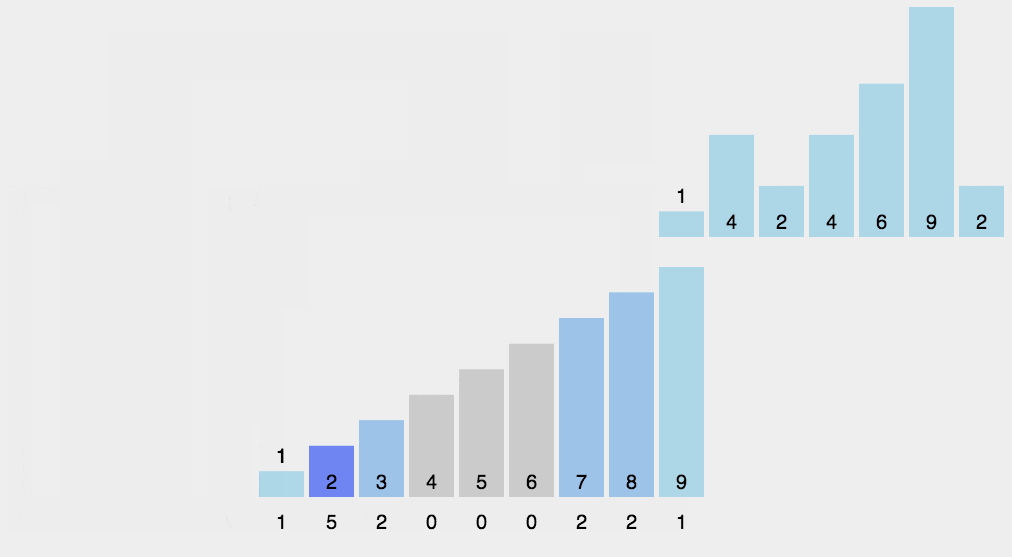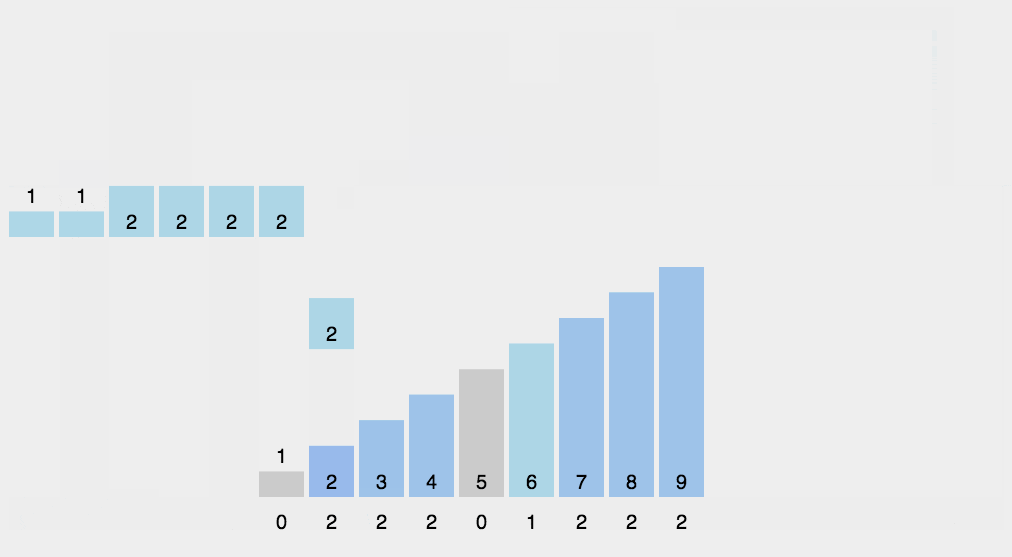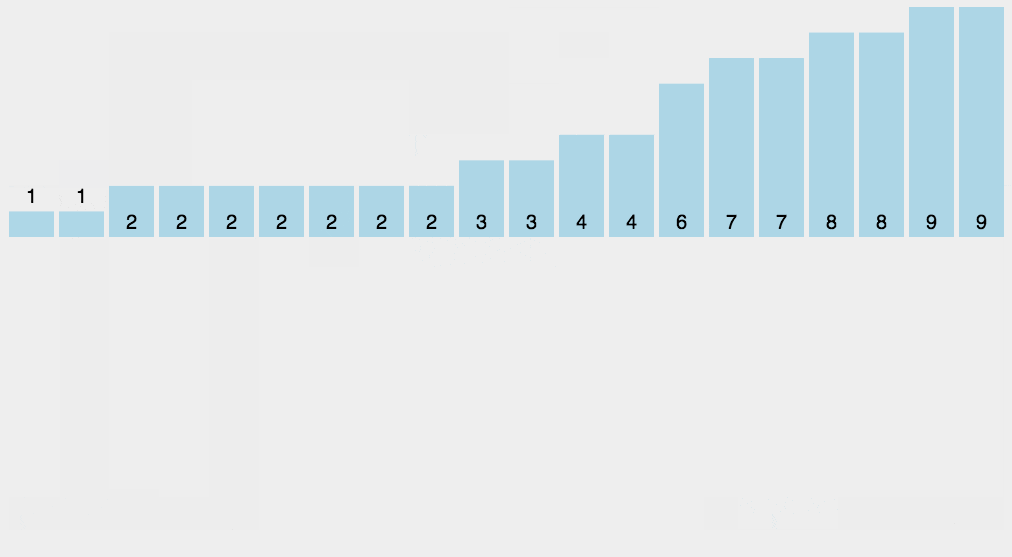
算法实现:
1 | |
Bucket Sort
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效,我们需要做到这两点:
- 在额外空间充足的情况下,尽量增大桶的数量
- 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中
同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要。
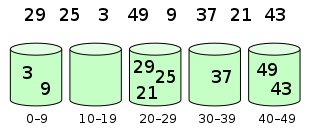

1 | |
LSD Radix Sort
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。
LSD 基数排序的基本步骤如下:
- 确定关键字的位数(即数字的最大位数)。
- 从最低有效位(最右边的位)开始,按照当前位的值进行稳定排序。
- 重复上述步骤,直到对所有位进行了排序。
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
- 基数排序:根据键值的每位数字来分配桶;
- 计数排序:每个桶只存储单一键值;
- 桶排序:每个桶存储一定范围的数值;

1 | |
My Thoughts
Coming soon
