BP神经网络

神经网络的构成

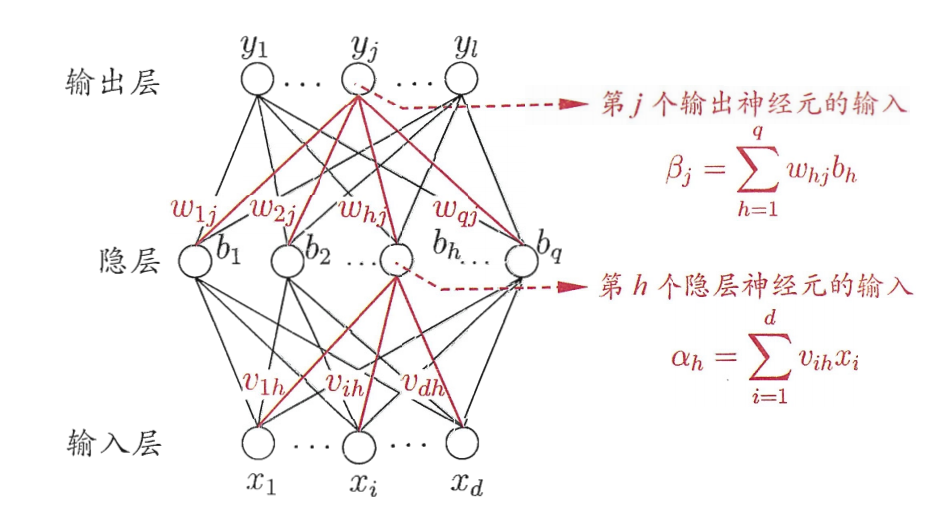
人工神经网络（ANN）具有自学习、自组织、较好的容错性和优良的非线性逼近能力。

在实际应用中，80%~90%的人工神经网络模型是采用误差反传算法或其变化形式的网络模型。

ANN通过数学近似映射（函数逼近）完成拟合——>预测，分类——>聚类分析的工作

从模型上进行拆分，神经网络包括：

1. 神经元模型
2. 激活函数
3. 网络结构
4. 工作状态
5. 学习方式

建立和应用神经网络的步骤

1. 网络结构的确定

   包含网络的拓扑结构和每个神经元相应函数的选取。

2. 权值和阈值的确定

   通过学习得到，利用已知的一组正确的输入输出，调整权值和阈值使得网络输出与理想输出偏差尽量小。

3. 工作阶段

   用带有确定权重值和阈值的神经网络解决问题的过程，也叫模拟。

人工神经元的模型

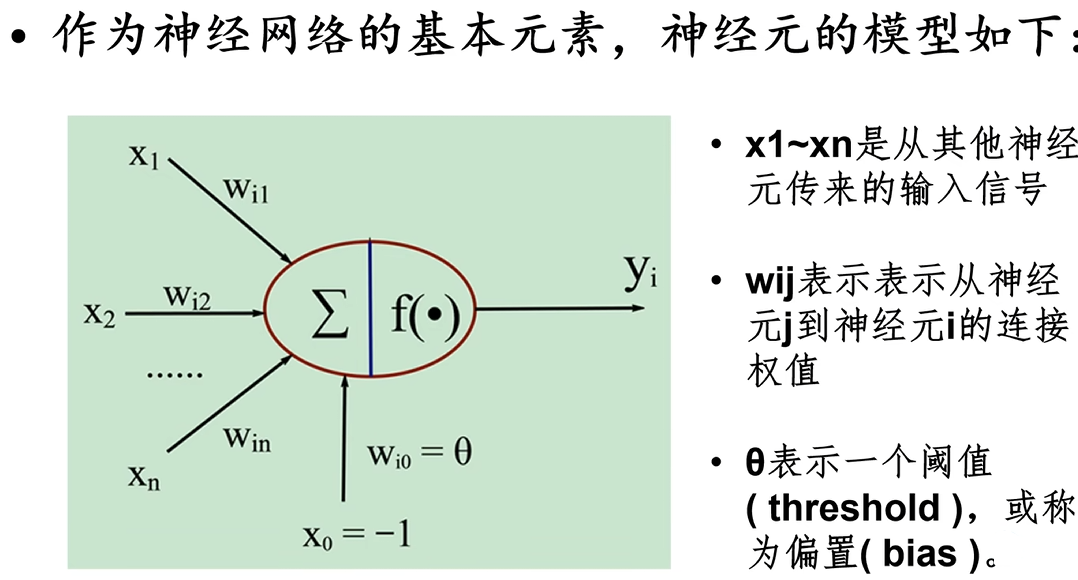
• 神经元输入与输出的关系为：

$$
net_{i}=\sum_{j=1}^{n}w_{ij}x_{j}-\theta =\sum_{j=0}^{n}w_{ij}x_{j} \\
y_{i}=f(net_{i})
$$

• 若用X表示输入向量，W表示权重向量

$$net_{i}=XW,y_{i}=f(XW)$$

• 常用激活函数

1. 线性函数
   $$f(x)=kx+c$$

2. S函数
   $$f(x)=\frac{1}{1+e^{-ax}}$$

3. 阈值函数
   $$f(x)=\begin{cases} T,x>c\\ kx,-c\le x\le c \\ -T,x<-c \end{cases}$$

4. 双极S函数
   $$f(x)=\frac{2}{1+e^{-ax}}-1$$

网络模型

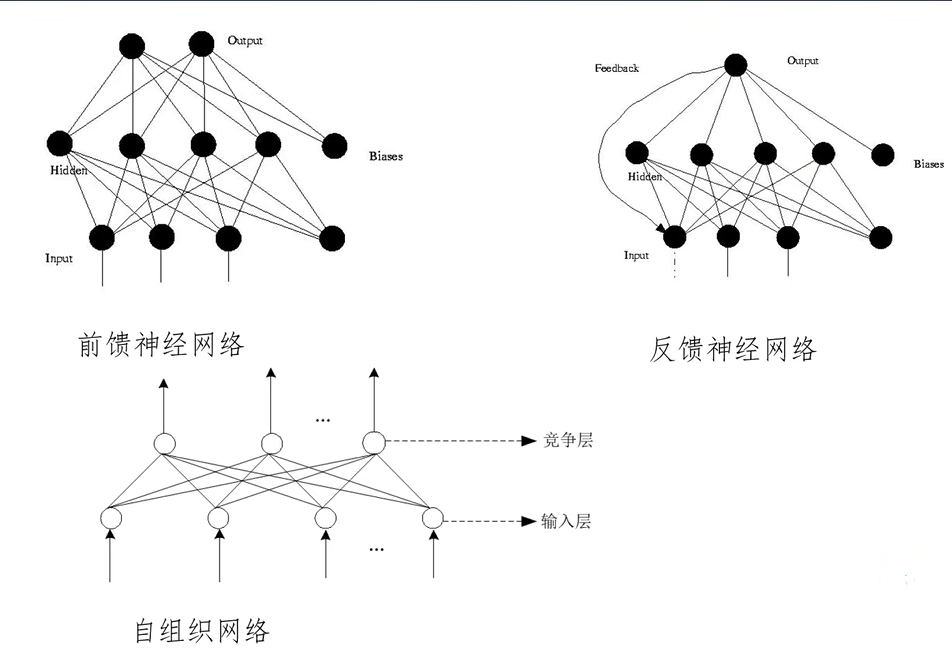
1. 前馈神经网络

   只在训练过程会有反馈信号，而在分类过程中数据只能向前传送，直到到达输出层

2. 反馈神经网络

   从输出到输入过程具有反馈链接的神经网络

3. 自组织神经网络

   通过自动寻找样本中的内在规律和本质属性，自组织、自适应地改变网络参数与结构。

学习方式

1. 有监督学习

将一组训练集送入网络，根据网络的实际输出与期望输出之间的差别来调整连接权

2. 无监督学习

抽取样本中蕴含的统计特征，并以神经元之间的连接权的方式存于网络中。

采用BP学习算法的前馈神经网络称为BP神经网络

BP算法

BP(Back Propagation)算法的基本原理

利用输出后的误差来估计输出层的直接前导层的误差，再用这个误差估计更前一层的误差，获得各层的误差估计。

总结来说，就是信号的正向传播&误差的反向传播

案例

1981年生物学家发现了两类蚊子，他们测量的数据如下

翼长	触角长	类别
1.78	1.14	Apf
1.96	1.18	Apf
1.86	1.20	Apf
1.72	1.24	Af
2.00	1.26	Apf
2.00	1.28	Apf
1.96	1.30	Apf
1.74	1.36	Af
1.64	1.38	Af
1.82	1.38	Af
1.90	1.38	Af
1.70	1.40	Af
1.82	1.48	Af
1.82	1.54	Af
2.08	1.56	Af

构建模型区分两种蚊子。

以触角和翼长为坐标轴作图

x为触角长，y为翼长

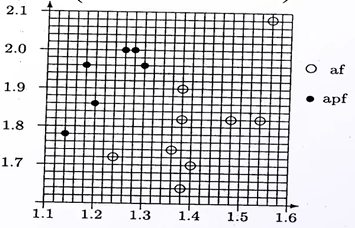
思路一：做一条直线将两类蚊子区分开

$$y=1.47x-0.017$$

分类规则：在直线一侧的便归为那一类。

思路二：将问题看为一个系统，构建一个神经网络训练模型

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score

# 创建数据框
data = {
    '翼长': [1.78, 1.96, 1.86, 1.72, 2.00, 2.00, 1.96, 1.74, 1.64, 1.82, 1.90, 1.70, 1.82, 1.82, 2.08],
    '触角长': [1.14, 1.18, 1.20, 1.24, 1.26, 1.28, 1.30, 1.36, 1.38, 1.38, 1.38, 1.40, 1.48, 1.54, 1.56],
    '类别': ['Apf', 'Apf', 'Apf', 'Af', 'Apf', 'Apf', 'Apf', 'Af', 'Af', 'Af', 'Af', 'Af', 'Af', 'Af', 'Af']
}
df = pd.DataFrame(data)

# 将类别转换为数值编码
df['类别'] = df['类别'].map({'Apf': 0, 'Af': 1})

# 准备训练集和测试集
X = df[['翼长', '触角长']]
y = df['类别']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建并训练决策树模型
clf = DecisionTreeClassifier(random_state=42)
clf.fit(X_train, y_train)

# 在测试集上进行预测
y_pred = clf.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("准确率：", accuracy)