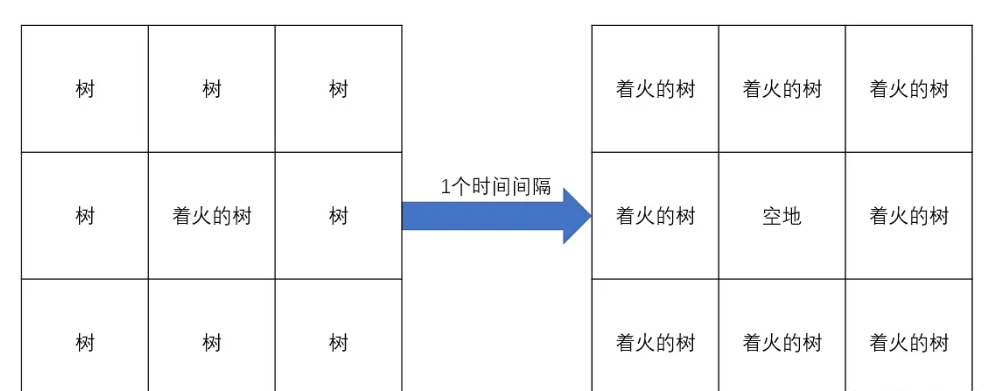
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
| close all;
clc;
clear;
figure;
p=0.3;
f=6e-5;
axes;
rand('state',0);
set(gcf,'DoubleBuffer','on');
S=round(rand(300)*2);
Sk=zeros(302);
Sk(2:301,2:301)=S;
C=zeros(302,302,3);
R=zeros(300);
G=zeros(300);
R(S==2)=1;
G(S==1)=1;
C(2:301,2:301,1)=R;
C(2:301,2:301,2)=G;
Ci=imshow(C);
ti=0;
tp=title(['T = ',num2str(ti)]);
while 1
ti=ti+1;
St=Sk;
St(Sk==2)=0;
Su=zeros(302);
Sf=Sk;
Sf(Sf<1.5)=0;
Sf=Sf/2;
Su(2:301,2:301)=Sf(1:300,1:300)+Sf(1:300,2:301)+Sf(1:300,3:302) +...
Sf(2:301,1:300)+Sf(2:301,3:302)+Sf(3:302,1:300) + ...
Sf(3:302,2:301)+Sf(3:302,3:302);
St((Su>0.5)&(Sk==1))=2;
Se=Sk(2:301,2:301);
Se(Se<0.5)=4;
Se(Se<3)=0;
Se(Se>3)=1;
St(2:301,2:301)=St(2:301,2:301)+Se.*(rand(300)<p);
Ss=zeros(302);
Ss(Sk==1)=1;
Ss(2:301,2:301)=Ss(1:300,1:300)+Ss(1:300,2:301)+Ss(1:300,3:302) +...
Ss(2:301,1:300)+Ss(2:301,3:302)+Ss(3:302,1:300) + ...
Ss(3:302,2:301)+Ss(3:302,3:302);
Ss(Ss<7.5)=0;
Ss(Ss>7.5)=1;
d=find(Ss==1 & Sk==1);
for k=1:length(d)
r=rand(1);
St(d(k))=round(2*(r<=f)+(r>f));
end
Sk=St;
R=zeros(302);
G=zeros(302);
R(Sk==2)=1;
G(Sk==1)=1;
C(:,:,1)=R;
C(:,:,2)=G;
set(Ci,'CData',C);
set(tp,'string',['T = ',num2str(ti)]);
pause(1);
end
|