插值与拟合

插值问题

当我们遇到“已知函数在某区间内若干点处的值，求函数在该区间（域）内其他点处的值”这种问题使，我们可以考虑使用插值法解决。

常用的插值法有Lagrange插值法和Newton插值法。

Lagrange插值法

拉格朗日插值公式指的是在节点上给出节点基函数，然后做基函数的线性组合，组合系数为节点函数值的一种插值多项式。

$$f(x)=\sum_{i=0}^{k}y_{i}\prod_{j\ne i}\frac{x-x_{j}}{x_{i}-x_{j}}$$

在高次插值时，我们需要考虑高次插值的Runge现象

当插值次数超过七次时，插值多项式会出现严重的振荡现象，称为Runge现象。

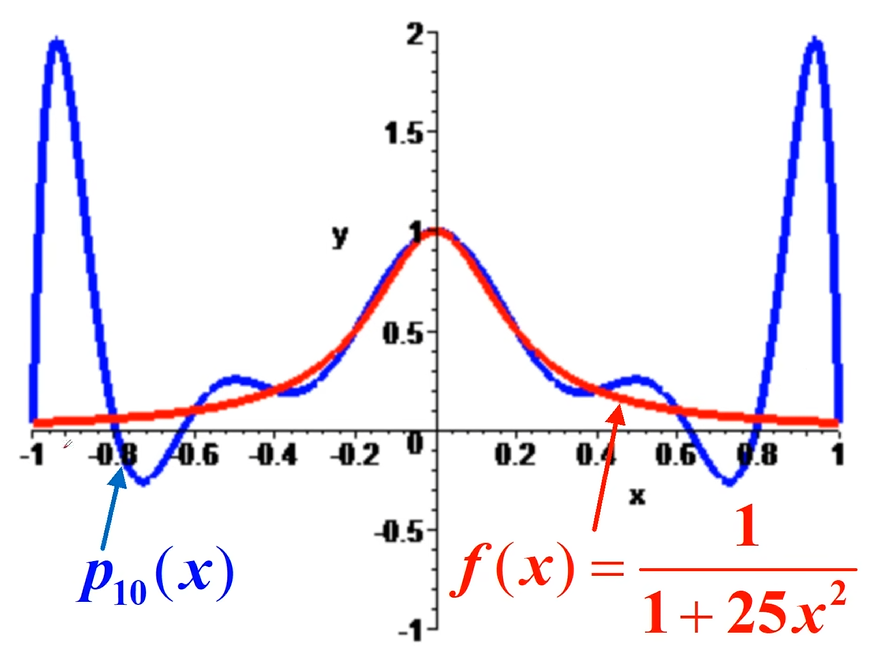
避免方法为：将插值区间分为若干小区间，在小区间内用低次插值

MATLAB的使用

基本命令：

yi=interp1(x,y,xi,'method') %一维插值

zi=interp2(x,y,z,xi,yi,'method') %二维插值

x,y为插值点，xi,yi为被插值点和插值结果,通常为向量；’method’表示插值方法：’nearest’——最邻近插值，’linear’——线性插值 ，’spline’——三次样条插值， ‘cubic’——立方插值。

拟合问题

插值和拟合的区别：

1. 插值函数一定过已知点，拟合函数不一定过已知点

2. 插值主要求函数值，拟合主要求函数关系

拟合的计算

曲线拟合需要解决如下两个问题：

1. 线型的选择（根据散点图选择合适的函数模型）

2. 线型中参数的计算

MATLAB的使用

1. 多项式拟合

[a,S]=polyfit(x,y,n)

其中x和y是被拟合数据的自变量和因变量，n为拟合多项式的次数，a为拟合多项式系数构成的向量，S为分析拟合效果所需的指标。