GRA
灰色系统的概念
灰色系统这个概念的是相对于白色系统和黑色系统而言的。
白色系统是指一个系统的内部特征是完全已知的,即系统的信息是完全充分的。
黑色系统是指一个系统的内部信息对外界来说是一无所知的,只能通过它与外界的联系来加以研究。
灰色系统介于两者之间,表示我们只对该系统有部分了解,系统内各因素间有不确定的关系。
灰色系统的应用范畴大致分为以下几方面:
- 灰色关联分析
- 灰色预测:人口、灾变等
- 灰色决策
- 灰色预测控制
灰色预测法
灰色预测法是一种对含有不确定因素的系统进行预测的方法。
其核心是在一定范围内变化的、与时间有关的灰色过程进行预测。
灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,建立相应的微分方程模型。
灰色预测的四种常见类型
灰色时间序列预测
用观察到的反应预测对象特征的时间序列来构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间
畸变预测
即通过灰色模型预测异常值出现的时刻,预测异常值什么时候出现在特定时区内
系统预测
通过对系统行为特征指标建立一组相互关联的灰色预测模型,预测系统中众多变量之间的相互协调关系的变化。
拓扑预测
将原始数据做曲线,在曲线上按定值寻找该定值发生的所有时点,并以该定值为框架生成时点数列,建立模型预测该定值所发生的时间点
灰色关联度与优势分析
我们分析一个系统时,需要对系统进行因素分析,找出主要和次要、促进和抑制、潜在和明显的因素。
事实上,因素之间关联性如何、关联程度如何量化等问题是系统分析的关键。
对于回归分析法来说,灰色关联度不需要大量的数据、计算量较小、反常情况影响小。
灰色关联度是分析向量与向量、矩阵与矩阵之间的关联度,需要选取参考数据。
灰色关联度的数学模型
首先也是最重要的,我们需要确定参考数列。我们假设参考数列为 $X_{0}$ ,有:
$$
X_{0}=(X_{0}(k) | k=1,2,\ldots,n)=(X_{0}(1),X_{0}(2),\ldots,X_{0}(n))
$$
其中 $k$ 表示时刻
假设有m个比较数列
$$
X_{i}=(X_{i}(k)|k=1,2,\ldots,n )=(X_{i}(1),X_{i}(2),\ldots,X_{i}(n))\\
(i=1,2,\ldots,n)
$$
则称
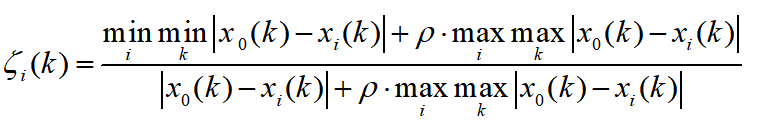
为灰色关联系数,其中 $\rho$ 称为分辨系数,一般取 $\rho = 0.5$ 。
由上式给出的定义在各个时刻都有一个关联系数,信息过于分散不易比较,因此我们给出
$$ r_{i}=\frac{1}{n} \sum_{k=1}^{n} \zeta_{i}(k) $$
为比较数列对参考数列的关联度。
由于公式研究的是关联系数的相对大小,无法判断是正相关还是负相关,我们记
$$
\sigma_{i}=\sum_{k=1}^{n}kX_{i}(k)-\sum_{k=1}^{n}X_{i}(k)\sum_{k=1}^{n}\frac{k}{n}
$$
$$
\sigma_{n}=\sum_{k=1}^{n}k^{2}-\frac{2(\sum_{k=1}^{n}k)}{n}
$$
$$sign(\frac{\sigma_{i}}{\sigma_{n}})=sign(\frac{\sigma_{j}}{\sigma_{n}})$$
称数列i与j为正相关,反之若不同号则为负相关。
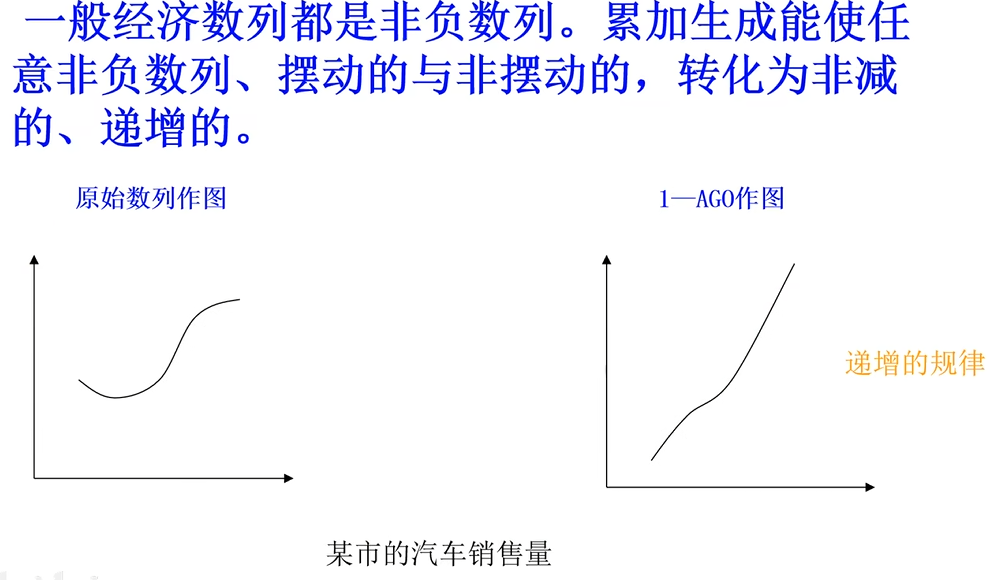
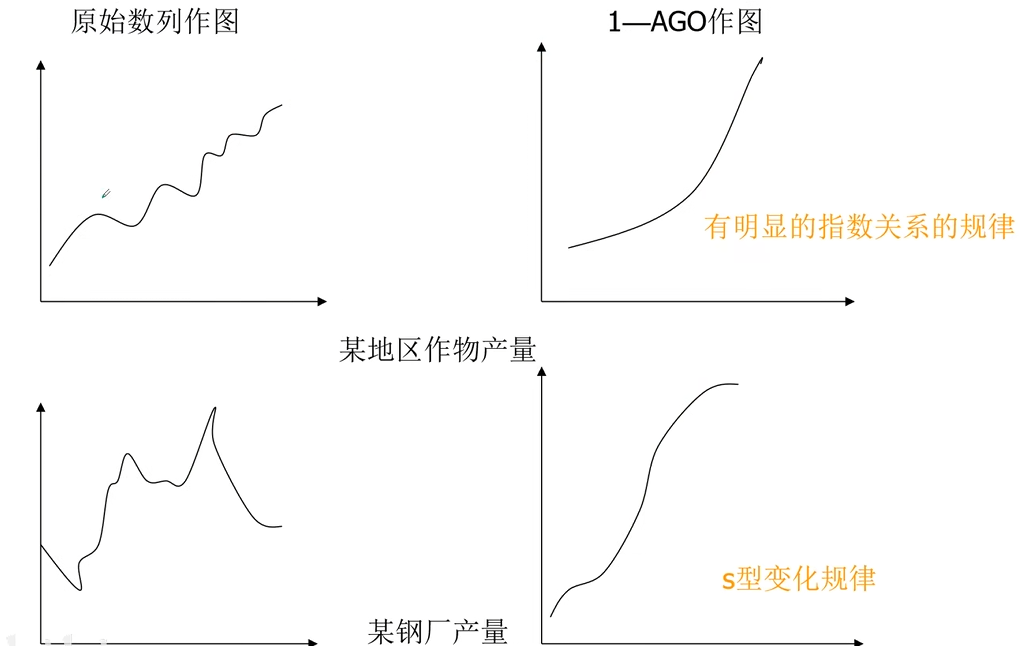
灰色生成数列
灰色序列常见的数据生成方法有:累加生成、累减生成和加权累加。
累加生成
把数列各项(时刻)数据依次累加的过程称为累加生成过程,由累加生成过程所得的数列称为累加生成数列。
若原始数列为 $x^{0}=(x^{0}(1),x^{0}(2),\ldots,x^{0}(n))$
令 $x^{1}(k)=\sum_{i=1}^{k}x^{0}(i)$ ,得到新数列,称为1次累加生成数列。
例如,数列 $(1,2,3,4)$ 经过累加处理得到 $(1,3,6,10)$
多次累加处理即可得到i次累加生成数列
累减生成
为累加过程的逆过程
由上述的数列 $x^{1}$ 累减得到的数列就是 $x^{0}$
在实际运用中,我们可以i在数列 $x^{1}$ 的基础上得到预测数列 $\hat x^{1}$ ,累减得到预测数列 $\hat x^{0}$ 。
不难看出,累减生成具有求导性质。
加权邻值生成
在原始数列中,相邻的两个数据称为前邻值和后邻值。对于常数 $\alpha$ ,令:
$$z^{0}(k)=\alpha x^{0}(k)+(1-\alpha)x^{0}(k-1)$$
得到的数列 $z^{0}$ 称为数列 $x^{0}$ 在权 $\alpha$ 下的邻值生成数, $\alpha$ 为生成系数。
当 $\alpha=0.5$ 时,也称均值生成数。
应用:便于将无规律的数据处理为有一定规律的数据。
灰色模型GM
灰色模型是利用离散随机数经过生成变为随机性被显著削弱而且有规律的生成数建立起的微分方程形式的模型,这样便于对其变化过程进行研究和描述。
设原始数列为 $x^{0}=(x^{0}(1),x^{0}(2),\ldots,x^{0}(n))$
一次累加数列为 $x^{1}=(x^{1}(1),x^{1}(2),\ldots,x^{1}(n))$
定义 $x^{1}$ 的灰导数为:
$$d(k)=x^{0}(k)=x^{1}(k)-x^{1}(k-1)$$
令 $z^{1}$ 为数列 $x^{1}$ 的邻值生成数列,即
$$z^{0}(k)=\alpha x^{0}(k)+(1-\alpha)x^{0}(k-1)$$
于是定义GM的灰微分方程模型为
$$d(k)+az^{1}(k)=x^{0}(k)=az^{1}(k)=b$$
我们称a为发展系数,b为灰作用量。
将k代入可得:
$$\begin{cases}
x^{0}(2)=az^{1}(2)=b \\
x^{0}(3)=az^{1}(3)=b \\
\ldots \\
x^{0}(n)=az^{1}(n)=b
\end{cases}$$
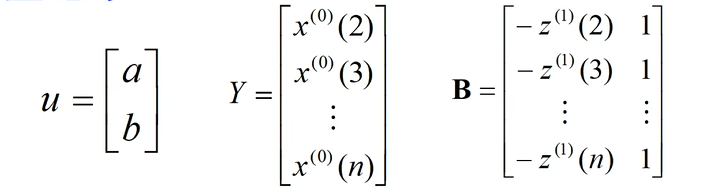
则该模型表示为 $Y=Bu$
用最小二乘法估计:
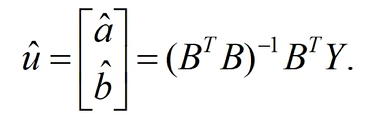
这样我们可以得到a、b的值。
之后,我们建立GM模型,得出对应的白化模型并求解。
白化模型为:
$$
\frac{dx^{1}(t)}{dt}+ax^{1}(t)=b
$$
通解为:
$$
x^{1}(t)=(x^{0}(1)-\frac{b}{a})e^{-a(t-1)}+\frac{b}{a}
$$
将t替换为k,即得到预测值。
数据的处理
在大部分情况下,我们需要对原始数据进行处理。
设原始数列为 $x^{0}=(x^{0}(1),x^{0}(2),\ldots,x^{0}(n))$
定义数列的级比:
$$
\lambda(k)=\frac{x^{0}(k-1)}{x^{0}(k)},k=2,3,\ldots,n
$$
如果所有的级比均落在可容覆盖区间 $X=(e^{\frac{-2}{n+1}},e^{\frac{2}{n+1}})$ 内,则数据可以建立GM模型。
否则需要对数据进行变换处理。
平移变换:取常数c,使数据列
$$y^{0}(k)=x^{0}(k)+C$$
让数据均落在区间内。
结果的检验
- 残差检验
定义相对残差:
$$
\varepsilon (k)=\frac{x^{0}(k)-\hat x^{0}(k)}{x^{0}(k)}
$$
根据实际情况界定残差的范围,一般要求 $\varepsilon(k) <0.2$
- 级比偏差值检验:
$$
\rho(k)=1-\frac{1-0.5a}{1+0.5a} \lambda (k)
$$
根据实际情况界定残差的范围,一般要求 $\rho(k) <0.2$