CA
聚类分析(CA)
聚类(Clustering)
聚类是将一个数据集划分为若干组(class)或类(cluster)的过程,使得同一组内的数据对象具有较高的相似度,而不同组的数据对象是不相似的。
相似和不相似是基于数据描述属性的取值来决定的,通常利用各数据对象之间的距离来表示。
聚类分析适用于探讨样本之间的相互关联关系从而对一个样本结构做一个初步的评价。
聚类和分类的区别:聚类是一种无监督的学习方法,不依赖于事先确定的数据类别以及标有数据类别的学习训练样本集合。
聚类分析的分类
聚类分析由两种组成:
- 对样品的分类,称为Q型
- 对变量(指标)的分类,称为R型
R型聚类分析的主要作用:
- 了解各个变量之间的亲疏程度,进行综合降维处理
- 根据变量的分类结果以及它们之间的关系,可以选择主要变量进行Q型聚类分析或回归分析
Q型聚类分析的主要作用:
- 可以综合利用多个变量的信息对样本进行分析。
- 分类结果直观,聚类谱系图清楚地表现数值分类结果。
- 聚类分析所得到的结果更为细致全面。
Q型聚类分析一般是我们研究的重点,Q型聚类的统计量一般是距离。
样品间的相似度量——距离
设有n个样本的p元观测数据:
$$x_{i}=(x_{i1},x_{i2},\ldots,x_{ip})^{T} , i=1,2,\ldots,n$$
这时,每一个样本可以看作p元空间的一个点,每两个点之间的距离记为 $d(x_{i},x_{j})$ 。
$$\begin{cases}
d(x_{i},x_{j})\ge 0,且 d(x_{i},x_{j})=0 当且仅当x_{i}=x_{j}\\
d(x_{i},x_{j})=d(x_{j},x_{i})
d(x_{i},x{j})\le d(x_{i},x_{k})+d(x_{k},x_{j})
\end{cases}$$
- 欧式距离
$$d(x_{i},x_{j})=\sqrt{\sum_{k=1}^{p}(x_{ik}-x_{jk})^{2}}$$
记为 $pdist(x)$
- 明式距离
$$d(x_{i},x_{j})=[{\sum_{k=1}^{p}(x_{ik}-x_{jk})^{m}}]^{\frac{1}{m}}$$
- 切式距离
$$d(x_{i},x_{j})=max\ \left| x_{ik}-x_{jk} \right | $$
变量之间的相似度量——相似系数
当对p个指标变量进行聚类时,用相似系数来衡量变量之间的相似程度(关联度)。
$$定义相似系数为 C_{\alpha \beta }$$
满足:
$$\begin{cases}
\left |C_{\alpha \beta } \right | \le 1 \\
C_{\alpha \alpha }=1 \\
C_{\alpha \beta }=\pm 1 当且仅当 \alpha=k \beta,k\ne 0 \\
C_{\alpha \beta }=C_{\beta \alpha}
\end{cases}$$
相似系数中最常用的是相关系数与夹角余弦。
- 夹角余弦
两变量的夹角余弦的定义为:
$$C_{ij}=cos\ \alpha_{ij}= \frac{\sum_{t=1}^{n}x_{ti}x_{tj}}{\sqrt{\sum_{t=1}^{n}x_{ti}^{2}} \sqrt{\sum_{t=1}^{n}x_{tj}^{2}}}$$
- 相关系数
两变量的相关系数为:
$$C_{ij}= \frac{\sum_{t=1}^{n}(x_{ti}-\bar x_{i})(x_{tj}-\bar x_{j})}{\sqrt{\sum_{t=1}^{n}(x_{ti}-\bar x_{i})^{2}} \sqrt{\sum_{t=1}^{n}(x_{tj}-\bar x_{j})^{2}}}$$
类间距离
现在我们可以来计算两个类别之间的距离。
设 $d_{ij}$ 表示两个样品 $x_{i},x_{j}$ 之间的距离, $G_{p},G_{q}$ 表示两个类别,各自含有 $n_{p},n_{q}$ 个样品。
我们可以用两类中的样本之间的最短(最长)距离作为两类之间的距离。
重心距离:平均点之间的距离:
$$D_{pq}=\sqrt{(\bar x_{p}-\bar x_{q})^{T}(\bar x_{p}-\bar x_{q})}$$重心:每个维度的坐标均为所有坐标的算术平均数
类平均距离:
$$D_{pq}=\frac{1}{n_{p}n_{q}} \sum_{i\in G_{p}} \sum_{j\in G_{q}} d_{ij} $$
谱系聚类法的步骤
- 选择样本点之间距离的定义以及类间距离的定义
- 计算n个样本两两之间的距离,得到距离矩阵 $D=(d_{ij})_{n*n}$ ,D为实对称矩阵
- 构造个类,每个类只含有一个样本
- 合并符合类间距离定义要求的两个类为一个新类
- 重新计算类间距离,并重复上述步骤直到类数为1
- 画出聚类图
- 决定类的个数和类
下图为聚类谱系图的实例:

上图中,3,4在2.20处分为了一类G1,G1和5在2.21处分为了一类G2,1,2在11左右分为了一类G3,到最大值时G2和G3归为一类G0.
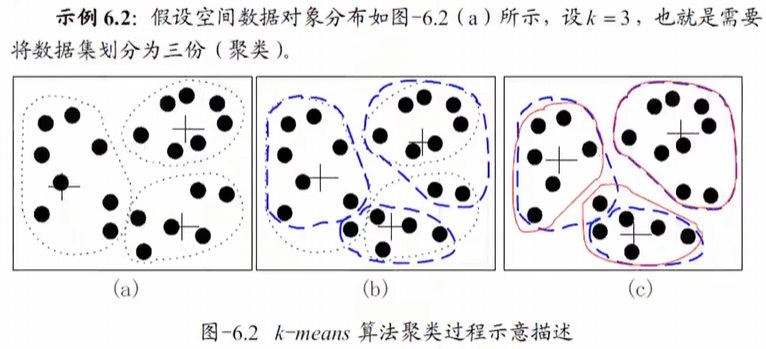
k——平均聚类算法
k-means算法
- 从n个数据对象中选择k个对象作为初始聚类中心
- 根据每个聚类对象的均值(中心对象),计算距离并根据最小距离重新对相应对象进行划分
- 更新中心对象
- 循环上述步骤一直到每个聚类不再变化
算法特点:
- 只适用于均值有意义的场所
- 对离群点和噪声数据敏感,极端效应严重