规划类问题

线性规划问题

在人们的生产实践中，经常会遇到如何利用现有资源来安排生产以取得最大效益的问题。

此类问题构成了运筹学的一个重要分支——数学规划，而LP（Linear Programming）则是其中的一个重要分支。

线性规划的基本形式

\begin{cases}
maxS = c_{1}x_{1}+c_{2}x_{2}+\ldots+c_{n}x_{n} = CX \ldots (1.1)\\
a_{11}x_{1}+a_{12}x_{2}+\ldots+a_{1n}x_{n} = b_{1} \\
a_{21}x_{1}+a_{22}x_{2}+\ldots+a_{2n}x_{n} = b_{2} \ldots (1.2)\\
\ldots \\
a_{n1}x_{1}+a_{n2}x_{2}+\ldots+a_{nn}x_{n} = b_{n}\\
\end{cases}

其中，$x_{i}\ge0$ , $b_{j}\ge0$ , $(i,j)\in(1,2,\ldots,n)^2$ , $C$ , $X$表示矩阵

变量 $X$ 称为决策变量，式(1.1)称为问题的目标函数，(1.2)中的几个不等式称为约束条件，记为s.t.

如果目标函数是求最小值 $minZ = CX$ ，令 $S=-Z$，则$maxS=-CX$。

线性规划问题的MATLAB求解

在MATLAB中，线性规划的目标函数默认为最小值，其规范形式为：

$$s.t.
\begin{cases}
Ax\le b\\
Aeq.x=beq\\
lb\le x \le ub\\
\end{cases}$$

其中， $c,x,b,beq,lb,ub$ 为列向量， $f$ 称为价值向量， $b$ 称为资源向量， $A,Aeq$ 为矩阵

MATLAB内置函数支持三种模式的线性规划问题的求解:

1
2
3

[x,fval] = linprog(c,A,b)
[x,fval] = linprog(c,A,b,Aeq,beq)
[x,fval] = linprog(c,A,b,Aeq,beq,lb,ub)

其中x返回的是决策变量的取值，fval返回的是目标函数的最优值，c为价值向量，A，b对应的是线性不等式约束，Aeq，beq对应的是线性等式约束，lb和ub对应决策向量的下界和上界。

一道例题

$$
max\ z=2x_{1}+3x_{2}-5x_{3}
$$

$$s.t.
\begin{cases}
x_{1}+x_{2}+x_{3}=7\\
2x_{1}-5x_{2}+x_{3}\ge 10\\
x_{1}+3x_{2}+x_{3}\le 12\\
x_{1},x_{2},x_{3}\ge 0
\end{cases}$$

MATLAB代码如下：

f=[-2;-3;5];
a=[-2,5,-1;1,3,1];
b=[-10;12];
aeq=[1,1,1];
beq=7;
[x,y]=linprog(f,a,b,aeq,beq,zeros(3,1));
x,y=-y

可转化为线性规划的问题

规划问题为

$$min\ \left| x_{1} \right|+\left| x_{2} \right|+ \ldots + \left| x_{n} \right|\\
s.t.\ Ax\le b$$

其中 $x=\begin{bmatrix}x_{1}&\ldots&x_{n} \end{bmatrix}^{T}$

事实上，我们可以进行如下处理：

取 $$u_{i}=\frac{x_{i}+\left| x_{i} \right|}{2}$$

$$v_{i}=\frac{-x_{i}+\left| x_{i} \right|}{2}$$

这样就把上面的问题转化为了：

$$
min\ \sum_{i=1}^{n}(u_{i}+v_{i})
$$

$$s.t.
\begin{cases}
A(u-v)\le b\\
u,v\ge 0\\
\end{cases}$$

审题到建模全过程分析

市场上有n种资产 $s_{i}$ （i=1,2,L,n）可供选择，现用数额为M的相当大的资金作为一个时期的投资。这种n资产在这一时期内购买 $s_{i}$ 的平均收益为 $r_{i}$ ，风险损失率为 $q_{i}$ ，投资越分散，总的风险越少，总体风险可用投资的 $s_{i}$ 最大的一个风险来度量。

购买 $s_{i}$ 时需要交付交易费，费率为 $p_{i}$ ，当购买额不超过给定值 $u_{i}$ 时，交易费按购买 $u_{i}$ 计算。另外，假定同期银行存款利率时 $r_{0}$ ，既无交易费又无风险。（$r_{0}$=5%）。n=4时，相关数据如下表：

$s_{i}$	$r_{i}$(%)	$q_{i}$(%)	$p_{i}$(%)	$u_{i}$(元)
$u_{i}$	28	2.5	1	103
$s_{2}$	21	1.5	2	198
$s_{3}$	23	5.5	4.5	52
$s_{4}$	25	2.6	6.5	40

试给该公司设计一种投资组合方案，即给定资金M，有选择地购买若干种资产或存银行生息，使净收益尽可能大，使总体风险尽可能小。

符号规定

$s_{i}$ 表示第i种投资项目，如股票，债券等，$i=0,1,L,n$,其中 $s_{0}$ 指存入银行；$r_{i},p_{i},q_{i}$ 分别表示 $s_{i}$ 的平均收益率、交易费率、风险损失率，$i=0,L,n$,其中 $p_{0}=0,q_{0}=0$，
$u_{i}$ 表示 $s_{i}$ 的交易定额，$i=1,L,n;x_{i}$ 表示投资项目 $s_{i}$ 的资金，$i=0,1,L,n$ ; $a$ 表示投资风险度，$Q$ 表示总体收益。

基本假设

投资数额M相当大，假设M=1
投资越分散，总风险越小
总体风险用投资项目 $s_{i}$ 中最大的一个来衡量
n+1种资产之间相互独立
投资期间各项利率为定值
净收益和总体风险不受其他因素影响

基于假设抽象出数学模型

1.总体风险用最大的一个来衡量，即：

$$max{q_{i}x_{i}|i=1,2,L,n}$$

2.购买 $s_{i}$ 所附的交易费是一个与 $x_{i}$ 相关的函数，即：

$$f(x)=
\begin{cases}
p_{i}x_{i},x_{i}\ge u_{i} \\
\\
p_{i}u_{i},x_{i}\le u_{i} \\
\end{cases}$$

而题目所给的定值 $u_{i}$ 相对总投资很小，所以购买 $s_{i}$ 都收益可以简化为 $(r_{i}-p_{i})x_{i}$。

3.要使净收益尽可能打，总体风险尽可能小，这是一个多目标规划模型，需要转化。

目标函数为：

$$\begin{cases}
max\ \sum_{i=0}^{n}(r_{i}-p_{i})x_{i} \\
\\
min{max{q_{i}x_{i}}}
\end{cases}$$

约束条件为：

$$\begin{cases}
\sum_{i=0}^{n}(1+p_{i})x_{i}=M \\
\\
x_{i}\ge 0, i=0,1,\ldots n\\
\end{cases}$$

模型一：固定风险水平，最大化优化收益

给定一个风险界限a，使最大的一个风险满足条件，这样就可以找到相应的投资方案。

$$
max\ \sum_{i=0}^{n}(r_{i}-p_{i})x_{i}
$$

$$s.t.
\begin{cases}
\frac{q_{i}x_{i}}{M} \le a \\
\\
\sum_{i=0}^{n}(1+p_{i})x_{i}=M \\
\end{cases}$$

代入数据可得到以下公式：

$$
min\ f=(-0.05,-0.27,-0.19,-0.185,-0,185)(x_{0},x_{1},x_{2},x_{3},x_{4})^{T}
$$

$$s.t.
\begin{cases}
x_{0}+1.01x_{1}+1.02x_{2}+1.045x_{3}+1.065x_{4}=1\\
0.025x_{1}\le a\\
0.015x_{2}\le a\\
0.055x_{3}\le a\\
0.026x_{4}\le a\\
x_{i}\ge 0
\end{cases}$$

由于a是任意给定的风险度，我们可以从a=0开始，以步长 $\Delta a=0.001$ 进行循环搜索,程序如下：

clc,clear
a=0;
hold on
while a<0.05
    c=[-0.05,-0.27,-0.19,-0.185,-0.185];
    A=[zeros(4,1),diag([0.025,0.015,0.055,0.026])]
    b=a*ones(4,1);
    Aeq=[1,1.01,1.02,1.045,1.065];
    beq=1;
    LB=zeros(5,1);
    [x,Q]=linprog(c,A,b,Aeq,beq,LB);
    Q=-Q;plot(a,Q,'*k');
    a=a+0.001;
end
xlabel('a'),ylabel('Q')

得到如下图形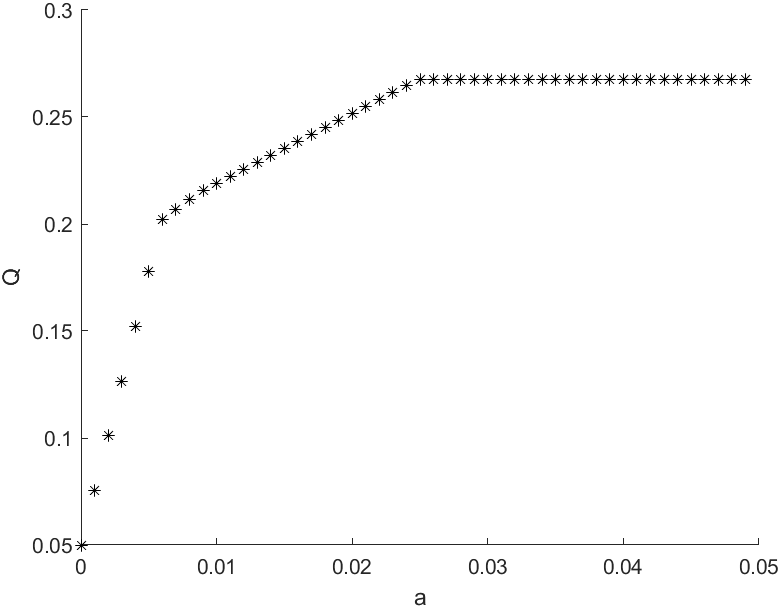

分析图形可知，随着风险度提升，收益上升。其中有两个拐点我们可以重点关注：
a=0.006和a=0.025
可以结合接下来的模型进一步分析。

模型二：固定盈利水平，极小化风险

$$
min (max {q_{i}x_{i}})
$$

$$s.t
\begin{cases}
\sum_{i=0}^{n}(r_{i}-p_{i})x_{i} \ge k\\
\\
\sum_{i=0}^{n}(1+p_{i})x_{i}=M \\
\end{cases}$$

模型三：对风险和收益赋给权重s和（1-s），s称为投资偏好系数。

$$
min\ (s*{max{q_{i}x_{i}}}) -(1-s) \sum_{i=0}^{n}(r_{i}-p_{i})x_{i}
$$

$$
s.t.\ \sum_{i=0}^{n}(1+p_{i})x_{i}=M
$$

整数规划模型

若数学规划中的变量（部分或全部）限制为整数时，称为整数规划。若在线性规划模型中，变量限制为整数，则称为整数线性规划（IP）。目前话没有一种方法能有效地求解一切整数规划。

整数规划有下面一些特点：

原线性规划最优解全是整数，则整数规划与线性规划最优解一致。
整数规划无可行解。
有可行解，但最优解变差。
整数规划求最优解不能按照实数最优解简单取整所得。

依照决策变量取证要求的不同，整数规划可分为纯整数规划、全整数规划、混合整数规划、0-1整数规划。

纯整数规划

所有决策变量要求取非负整数。
全整数规划

除了所有决策变量要求非负整数外，系数 $a_{ij}$ 和常数 $b_{i}$ 也要求取整数。
混合整数规划

只有一部分决策变量要求取非负整数。
0-1整数规划

所有决策变量只能取0或1两个整数。

整数线性规划的求解方法

设整数规划问题如下：

$$
max\ z = x_{1}+x_{2}
$$

$$\begin{cases}
14x_{1}+9x_{2}\le 51 \\
-6x_{1}+3x_{2}\le 1 \\
x_{1},x_{2}\ge 0 且为整数 \\
\end{cases}$$

首先不考虑整数约束，得到线性规划问题（一般称为松弛问题或伴随问题）

得出图像如下：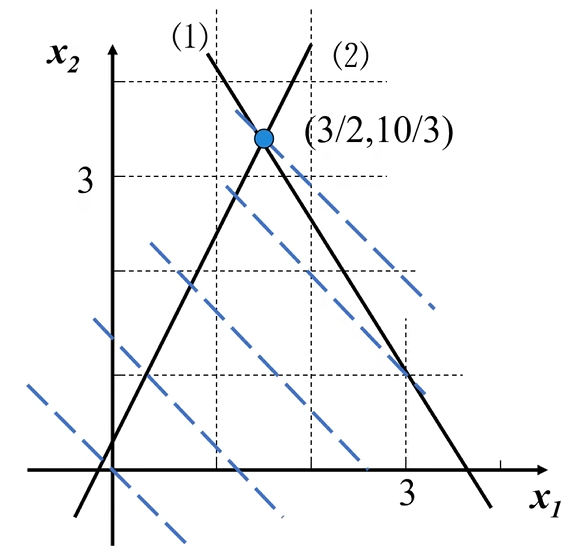

在解集内的所有整数点找出，一一带入，求出最优解，此法为完全枚举法，适用于约束条件较小的情况。

目前，常用的求解整数规划的方法：分枝定界法、割平面法；对于特殊的0-1规划问题采用隐枚举法和匈牙利算法。

分枝定界法

首先不考虑整数限制求出相应的松弛问题的最优解，若松弛问题无可行解，则ILP无可行解。

若求得的松弛问题最优解符合证书要求，则是ILP的最优解。

若不满足整数条件，则任选一个不满足整数条件的变量 $x_{i}^{0}$ 来构造新的约束条件添加到松弛问题中形成两个子问题（分别添加）：

$$
x_{i}\le \left [ x_{i}^{0} \right ] ; x_{i} \ge \left [ x_{i}^{0} \right ]+1
$$

依次在缩小的可行域中求解新构造线性规划的最优解，并重复上述过程直到子问题无解或有整数最优解。

割平面算法

割平面算法的基本思想：

如果松弛问题无解，则整数规划无解
如果松弛问题的最优解为整数向量，则其也是整数规划的最优解
如果解含有非整数分量，则对松弛问题添加线性约束条件来进行“割平面”操作，重复操作直到求出解或无解。

$$
max\ z=x_{1}+x_{2}
$$

$$\begin{cases}
-x_{1}+x_{2}\le 1 \\
3x_{1}+x_{2}\le 4 \\
x_{1},x_{2} \ge 0 且为整数
\end{cases}$$

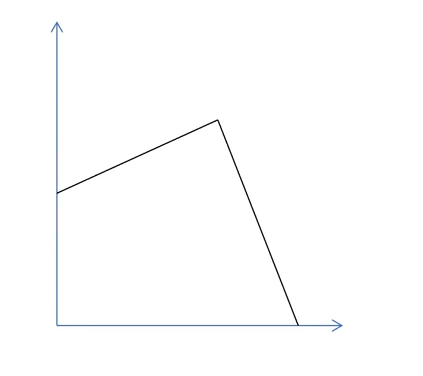
此时松弛问题的最优解不是整数，故我们分析图像可知：y轴截距做平行线上面的部分无法满足整数解，故舍去，体现在约束条件为 $x_{2}\le 1$ 。

对于一些问题，我们也可以利用引入松弛变量来将不等式的约束条件转化为等式约束条件。

在上题，我们可以引入松弛变量 $x_{3},x_{4}$ 来将不等约束转化为等式约束：

$$
max\ z=x_{1}+x_{2}+0x_{3}+0x_{4}
$$

$$\begin{cases}
-x_{1}+x_{2}+x_{3}=1 \\
3x_{1}+x_{2}+x_{4}=4 \\
x_{1},x_{2},x_{3},x_{4} \ge 0 且为整数
\end{cases}$$

这样我们可以得到一个等式，将各变量的系数拆分为整数部分和小数部分。可以取 $x_{3},x_{4}$ 为自由变量，考虑利用线性代数的知识得出基础解系，再在基础解系中找出整数解。

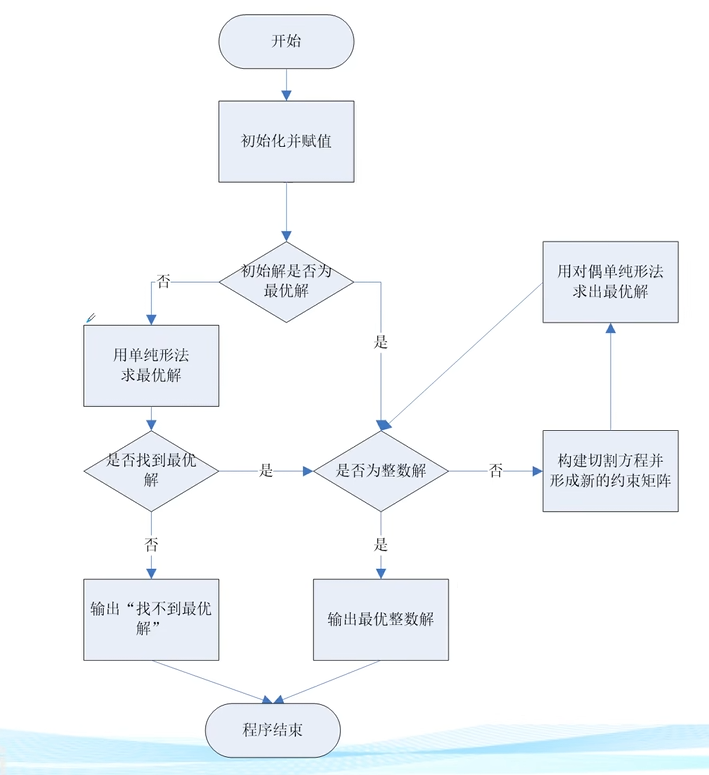
匈牙利算法解决0-1规划问题

$e.g.1$ 现有如下投资问题：

有600万元投资五个项目，收益如表，求利润最大的方案

项目	投资额	项目收益
I	210	160
II	300	210
III	150	60
IV	130	80
V	260	180

约束条件：项目I、II、III中选一项；项目III、IV中选一项；项目V以项目I为先验条件。

我们假设 $x_{i}= \begin{cases} 1 ,选中第i项 \\ 0 不选第i项 \end{cases}$

则可以抽象出下列模型：

$$
max\ Z=160x_{1}+210x_{2}+60x_{3}+80x_{4}+180x_{5}
$$

$$s.t.
\begin{cases}
210x_{1}+300x_{2}+150x_{3}+130x_{4}+260x_{5}\le 600 \\
x_{1}+x_{2}+x_{3}=1 \\
x_{3}+x_{4}=1 \\
x_{5}\le x_{1} \\
x_{1},x_{2},x_{3},x_{4},x_{5}=0 or 1\\
\end{cases}$$

$e.g.2$ 指派问题

甲乙丙丁四个人，ABCD四项工作，要求每人只能做一项工作，每项工作只由一人完成，问如何让指派总时间最短？

人员/时间/任务	A	B	C	D
甲	3	5	8	4
乙	6	8	5	4
丙	2	5	8	5
丁	9	2	5	2

引入0-1变量 $x_{ij}$
$x_{ij}=1 : 第 i 人做第 j 项工作$
$x_{ij}=0 ：第 i 人不做第 j 项工作$

$$
min\ Z=3x_{11}+5x_{12}+8x_{13}+4x_{14}+6x_{21}+8x_{22}+5x_{23}+4x_{24}+2x_{31}+5x_{32}+8x_{33}+5x_{34}+9x_{41}+2x_{42}+5x_{43}+2x_{44}
$$

每项任务只由一个人完成、每人只完成一项任务：每行每列之和均为1，即：
$$s.t.
\begin{cases}
\sum_{i=1}^{n}x_{ij}=1 \\
\\
\sum_{j=1}^{n}x_{ij}=1 \\
\\
x_{ij}=0 or 1 \\
\end{cases}$$

一些特殊情况的处理：

人少工作多：添加虚拟的“人”，代价都为0
人多工作少：添加虚拟的工作，代价都为0
一个人可做多件工作：该人变为几个相同的“人”
某工作一定不能有某人做：该人做该工作的相应代价取足够大M

指派问题的匈牙利解法的一般步骤：

第一步：变换指派问题的系数矩阵 $(c_{ij})$ 为 $(b_{ij})$ ，使在 $(b_{ij})$ 的各行各列中都出现0元素，即：
- 从 $(c_{ij})$ 的每行元素中都减去该行的最小元素
- 再从所得新系数矩阵的每列元素中减去该列的最小元素
  
  其中， $(c_{ij})$ 为每行每列仅有一个1的矩阵
进行试指派，以寻求最优解
- 在 $(b_{ij})$ 中尽可能寻找多的独立0元素，若能找出n个独立0元素，就以这n个独立0元素对应解矩阵 $(x_{ij})$ 中的元素为1，其余为0，这就得到最优解。
- 从只有一个0元素的行（列）开始，给这个0元素加圈，记作 O 。然后划去 O 所在列（行）的其它0元素，记作 X ，这表示这列所代表的任务已经指派完，不需要考虑他人。
- 给只有一个0元素的列（行）中的0元素加圈，划去所在行的0元素。
- 重复上述步骤直到尽可能多的0元素都被圈出和划掉。
若仍有没有画圈的0元素，且同行（列）的0元素至少有两个，则从剩下0元素最少的行（列）开始，比较他们列中0元素的数量，选择0元素少的那个0元素。

$$\begin{bmatrix}
3& 8& 2& 10&3 \\
8& 7& 2& 9&7 \\
6& 4& 2& 7&5 \\
8& 4& 2& 3&5 \\
9& 10& 6& 9&10
\end{bmatrix}$$

c=[3,8,2,10,3;8,7,2,9,7;6,4,2,7,5;8,4,2,3,5;9,10,6,9,10]
c=c(:) %将矩阵转化为向量
a=zeros(10,25);
for i=1:5
    a(i,(i-1)*5+1:5*i)=1;
    a(5+i,i:5:25)=1;
end  %循环将指派问题转化为线性规划问题
b=ones(10,1);
[x,y]=linprog(c,[],[],a,b,zeros(25,1),ones(25,1));
X=reshape(x,5,5)
opt=y

求得最优指派方案为 $x_{15}=x_{23}=x_{32}=x_{44}=x_{51}=1$，最优值为21.

非线性规划

一般形式：
$$
min\ f(x)
$$

$$s.t.
\begin{cases}
h_{j}(x)\le 0\ j=1,2,\ldots q \\
\\
g_{i}(x) = 0\ i=1,2,\ldots p
\end{cases}$$

在一组等式或不等式的约束下，求一个函数的最大值（或最小值）问题，其中至少有一个非线性函数，这类问题称之为非线性规划问题。

MATLAB中非线性规划的数学模型写成以下形式：

$$
min\ f(x)
$$

$$s.t.
\begin{cases}
A.x\le b \\
Aeq.x = beq \\
c(x) \le 0 \\
ceq(x) = 0 \\
lb\le x \le ub
\end{cases}$$

其中 $f(x)$ 是标量函数， $c(x),ceq(x)$ 是非线性向量函数。

二次规划

若某非线性规划的目标函数为自变量的二次函数，约束条件又全是线性的，就称这种规划为二次规划。
MATLAB中二次规划的数学模型可以表述如下：
$$
min\ \frac{1}{2}x^{T}Hx+f^{T}x
$$

$$s.t.
\begin{cases}
Ax\le b \\
Aeq.x=beq \\
lb \le x \le ub
\end{cases}$$

这里的H是实对称矩阵（二次型），f，b，beq，lb，ub是列向量，A，Aeq是相应维数的矩阵

MATLAB中二次规划的命令是
[x,fval]=quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)

一道例题

某公司有6个建筑工地要开工，每个工地的位置（用平面坐标系a，b表示，距离单位：KM）及水泥日用量d（吨）由下表给出。目前有两个临时料场位于A（5，1），B（2，7），日储量各有20吨。假设从料场导工地之间均有直线道路相连。

试制定每天的供应计划，即从A，B两料场分别向各工地运送多少吨水泥，使总的吨千米数最小
为了进一步减少吨千米数，打算舍弃两个临时料场，改建两个新的，日储量各为20吨，问应建在何处，使得节省的吨千米数最大？

工地位置(a,b)坐标参数以及水泥日用量d

	1	2	3	4	5	6
a	1.25	8.75	0.5	5.75	3	7.25
b	1.25	0.75	4.75	5	6.5	7.25
d	3	5	4	7	6	11

建立模型

我们可以记工地的位置为 $(a_{i},b_{i})$ ，水泥日用量为 $d_{i}$ ，料场的坐标为 $(x_{j},y_{j})$ 日储量为 $e_{j}$ ，从料场j向工地i的运送量为 $X_{ij}$ 。

目标函数为： $min\ f=\sum_{j=1}^{2} \sum_{i=1}^{6} X_{ij} \sqrt{(x_{j}-a_{i})^{2}+(y_{j}-b_{i})^{2}}$

$$s.t.
\begin{cases}
\sum_{j=1}^{2}X_{ij}=d_{i} \\
\\
\sum_{i=1}^{6}X_{ij}\le e_{j}
\end{cases}$$

当启用临时料场时决策变量为 $X_{ij}$ ，
不用临时料场时决策变量为： $X_{ij},x_{j},y_{j}$

来源：b站数模老哥，SJTU数模资料库。

MCM

#MCM

规划类问题

https://fabulous1496.github.io/2024/01/26/规划类问题/

作者

Fabulous

发布于

2024年1月26日

许可协议

AHP 上一篇

MCM绪论下一篇